12) Seja uma função polinomial não constante.
b) Se tem três raízes distintas em , prove que , para algum valor .
Passo 1
Cara, eu sei que exercícios como esse é muuuuuito confuso. Eu particularmente já me confundi muito. Mas aprendi uma técnica que me ajudou muito e vai te ajudar também! Então simbora!
A técnica é uma velha amiga nossa, o esboço. Desenhar em um gráfico o que está sendo falado. Então venha comigo!
Passo 2
Cara, imagina que existe uma função que zera em três pontos consecutivos , e . dessa forma aqui:
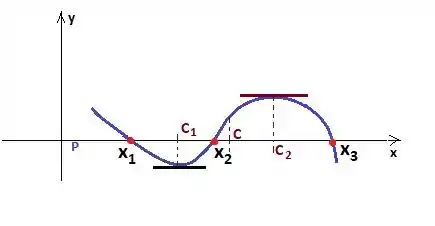
Tá vendo que existem dois pontos onde a derivada (reta tangente à curva) fica paralelo ao ? Isso significa que a derivada se anulou. Então entre e existe um ponto onde a derivada se anula
E entre e , existe outro ponto , onde a derivada também se anula:
Passo 3
Bem, o que queremos provar é que no intervalo de entre , existe um tal que a derivada segunda se anula, ou seja, que a curva troca de concavidade. Pelo desenho isso acontece, mas para provar isso, basta usar o Teorema de Rolle:
Resposta
Ei, a resposta está no passo a passo :)