Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Reta Tangente

Ver Teoria
Exercício 16123456789101112131415171819

Enunciado

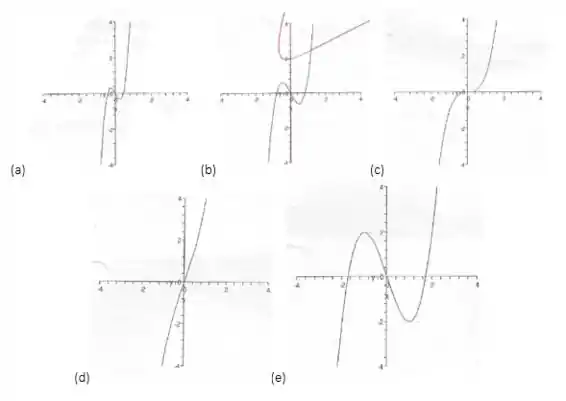
Aplicando os conceitos de derivada, qual o gráfico da função definida em R por f x = x 3 - 3 x ?

Passo 1

E aí, tudo beleza?

Vamos ver qual é o gráfico dessa função aqui:

f x = x 3 - 3 x

Bom, o exercício falou pra a gente usar os conceitos de derivada. A gente sabe que com a derivada podemos achar os pontos de máximo e mínimo da função, bem como os intervalos de crescimento e decrescimento. Bora lá então?

Passo 2

Bora derivar a função então! A gente vai usar a regra do Tombo: x n ' = n ⋅ x n - 1 .

Aplicando em f ( x ) :

f ' x = 3 ⋅ x 3 - 1 - 1 ⋅ 3 x 1 - 1

f ' x = 3 x 2 - 3 x 0

f ' x = 3 x 2 - 3

Passo 3

Bom, os pontos críticos da função, que são nossos candidatos a ponto de máximo e mínimo são os pontos onde a derivada é zero. Vamos ver isso igualando a derivada que acabamos de encontrar a zero, então:

f ' x = 0

3 x 2 - 3 = 0

3 x 2 = 3

x 2 = 3 3

x 2 = 1

x = ± 1

x = ± 1

Beleza! Esses são os pontos críticos da função😊

Passo 4

Vamos ver o valor da função nesses pontos agora. É só substituir os pontos na expressão da função. Um de cada vez e a gente vê qual o resultado:

f x = x 3 - 3 x

f - 1 = - 1 3 - 3 - 1 = - 1 + 3 = 2

f 1 = 1 3 - 3 1 = 1 - 3 = - 2

Olha só! Quando substituímos o - 1 nossa função deu 2 , e quando substituímos o 1 , nossa função de - 2 . Assim concluímos que temos um ponto de mínimo em ( 1 , - 2 ) e um ponto de máximo em ( - 1,2 ) !

Isso só acontece lá no último gráfico, na letra e , que é o gráfico da nossa função😉

Resposta

Letra (e).