Um pedaço de papel retangular é usado para construir uma caixa sem tampa, pra isso corta-se quadrados iguais de cada canto do papel. O papel retangular possui 8 centímetros de largura por 15 centímetros de comprimento. Determine o volume máximo para tal caixa.
- Aproximadamente 90,74;
- Exatamente 60;
- Aproximadamente 80;
- Aproximadamente 50;
- Nenhuma das respostas anteriores.
Passo 1
Vamos pensar no nosso retângulo, o enunciado nos mostra que ele é assim ó
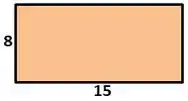
O enunciado nos disse que ele vai recortar quadrados nos quatro cantos, então teremos o seguinte:
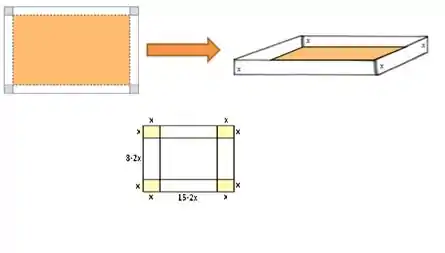
O volume dessa caixa, será:
Se você for observar bonitinho aquele desenho, vai ver que a altura vale , certo? A largura dela vale e o comprimento vale , então agora é substituir isso aí na nossa fórmula do volume.
Resolvendo as multiplicações, teremos:
Passo 2
Como ele pediu o maior volume possível da caixa, teremos que achar o valor máximo da função volume.
Para encontrarmos os pontos de máximo e mínimo, vamos fazer a primeira derivada e igualar ela a zero! Grava isso...máximo e mínimo, primeira derivada igual a zero
Derivando, teremos:
Observa que a derivada da soma é igual a soma das derivadas, certo? Então
Observa que deixei todas as constantes de fora da derivada.
Agora é só derivar tudo aí. Vamos lembrar a derivada de polinômio?
Então
Agora vamos igualar isso a zero e encontrar as raízes
Resolvemos essa equação do segundo grau pra ver onde que ela vale zero. Primeiro vem nosso delta
Detalhe, no nosso caso temos
Vamos jogar nas fórmulas, então. Primeiro calculando o delta
Ou seja, temos duas raízes:
Beleza, agora precisamos ver qual das duas nos dá o maior e o menor volume possível...
Vamos substituir esses valores na expressão que encontramos para o volume, essa aqui ó:
Primeiro o
Fazendo o
Esse obviamente, vamos descartar porque não faz sentido termos um volume negativo!
Sendo assim, o volume é proximo de ! Letra A!
Resposta
Letra A