Determine o ponto crítico da função
- 3 e 4
- Nenhuma das respostas anteriores
- 2 e 3
- 3
- 0
Passo 1
Fala aí, tudo beleza? Essa aqui é outra aplicação das derivadas!
Vamos encontrar um ponto crítico da função, que é um ponto bem especial.
A derivada representa a inclinação da reta tangente ao gráfico em determinado ponto. Chamamos de ponto crítico, um ponto que pode ser de máximo, ou de mínimo da nossa função. Nesses pontos a reta tangente fica na horizontal e não tem inclinação, com isso a derivada será igual a zero.
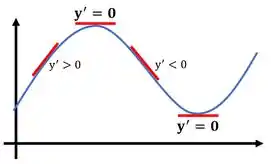
Por hora, vamos aprender a calcular esse ponto...
Então para determinarmos o ponto crítico, vamos encontrar a primeira derivada da nossa função e depois igualar ela a zero, vamos lá?
Passo 2
Nossa função é:
A gente deriva com a regra do Tombo, que a gente já aprendeu lá atrás, descendo o expoente pra frente e perdendo 1 no novo expoente. Vai ficar assim:
Como todo número elevado a zero é 1...
Essa é a nossa derivada!
Passo 3
Agora vamos igualar a derivada que achamos a zero ...
Prontinho! Esse é o nosso ponto crítico da função. Quer dizer que ele pode ser um ponto de valor máximo ou de valor mínimo! Como não sabemos qual dos dois, chamamos apenas de ponto crítico. 😉
Resposta
d) 3.