Uma pessoa dispõe de 900m de arame para cercar um terreno retangular. Utilizando o conceito de derivada, determine as dimensões deste terreno para que o mesmo apresente área máxima.
Passo 1
Beleza, a princípio temos um terreno com a seguinte cara:
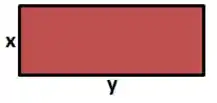
O que o problema quer que a gente descubra, são os valores de e de que fazem com que ele tenha a maior área possível. Então vamos descobrir quem é a função que descreve a área e encontrar os valores de e de que fazem seu valor ser máximo, pra isso usaremos os conceitos de derivada que estamos estudando.
O enunciado nos afirma que o cercado em preto é de 900 metros. Ou seja, o seu perímetro é
Podemos simplificar essa expressão, dividindo tudo por . Isso vai facilitar os nossos cálculos mais à frente.
Podemos isolar o e ficamos com
Dessa forma, as dimensões do terreno serão
Agora vamos falar sobre a área desse terreno. Ela é a multiplicação de um lado pelo outro, certo? Então
Prontinho, achamos a função que descreve a área desse terreno.
Passo 2
Para encontrarmos a maior área possível, vamos procurar o valor máximo da função área que a gente acabou de encontrar no passo anterior. Pra isso precisamos fazer a primeira derivada dela e depois igualar a zero. Lembra que pra acharmos os valores de máximos e mínimos nós fazemos a primeira derivada igual a zero? Então...isso que faremos agora.
Mãos a obra...
Achamos a derivada. Agora vamos igualar a zero e encontrar o valor de nesse ponto....
Agora vamos atrás do valor de .
Como vimos antes
Ou seja, esse nosso retângulo será na verdade um quadrado com lado , tendo a maior área possível de ser cercada com a quantidade de arame disponível.
Resposta
Quadrado com lado