Calcule a área da superfície obtida pela revolução da curva em torno do eixo no intervalo
Passo 1
Área de superfície de revolução, sabemos que aqui precisamos usar o Teorema de Pappus! Vamos fazer um esboço da curva e da superfície pra entender melhor o enunciado:
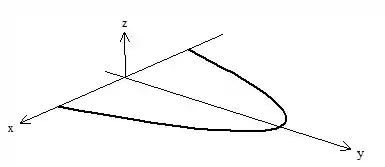
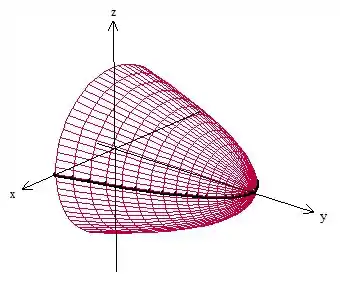
Perceba que não precisamos rotacionar completamente a curva para obter essa superfície! Lembra daquele caso em que a curva é simétrica em relação ao eixo? Isso acontece aqui também. Então, para calcular a área correta, precisamos fazer metade da rotação só, com isso:
Precisamos parametrizar a curva, tirar o módulo da integral, calcular e depois juntar tudo, beleza?
Passo 2
Uma parametrização simples da curva é a seguinte:
Passo 3
Vamos começar analisando quando a função x é positiva e quando é negativa:
Dado o intervalo que obtivemos, , vemos que é positivo no intervalo e negativo no intervalo , portanto:
Passo 4
Precisamos agora calcular o termo , para isso vamos derivar a nossa parametrização:
Passo 5
Juntando tudo na integral:
Em ambas integrais vamos fazer a seguinte substituição:
Ficamos com:
Podemos inverter a segunda integral se mudarmos o sinal né?