UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV2 - 2023.1, Questão 4
Calcule , onde e é a interseção do plano com o cilindro . (Oriente C no sentido anti-horário quando visto de cima).
Passo 1
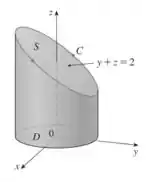
Olá meu caro amigo, saudades de você. Fico feliz que tenha voltado para estudar mais um pouco de cálculo. A curva C (uma elipse) está mostrada na Figura abaixo. Apesar de poder ser calculada diretamente, é mais simples usar o Teorema de Stokes. É sempre importante procurarmos caminhos mais facil, então vejamos
Passo 2
Vamos inicialmente calcular
Apesar de existirem muitas superfícies com fronteira C, a escolha mais conveniente é a
região elíptica S no plano cuja fronteira é C. Se orientarmos S para cima, em seguida, C tem a orientação induzida positiva. A projetação de D de S no plano xy será um disco , agora integrando
Resposta
Exercícios de Livros Relacionados
Como se integra uma função sobre uma superfície parametrizada no espaço? E de superfícies que são definidas implicitamente ou na forma explícita? O que se pode calcular com asintegrais de superfície?
Área de uma região elíptica - Encontre a área da região elíptica cortada do plano x + y + z = 1 pelo cilindro x 2 + y 2 = 1 .
Área de uma calota parabólica - Encontre a área da calota cortada do paraboloide y 2 + z 2 = 3 z pelo plano x = 1 .
Cilindro circular cortado por planos - Integre g x , y , z = x 4 y y 2 + z 2 sobre a porção do cilindro y 2 + z 2 = 25 que está no primeiro octante entre os planos x = 0 e x = 1 e acima do plano z = 3