UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV1 - 2022.1, Questão 3
Calcule a integral onde é a fronteira (orientada positivamente) da região delimitada pelas curvas e no primeiro quadrante.
Passo 1
Eaew, beleza?
Precisamos calcular a seguinte integral de linha
em que a curva é a fronteira da região entre as curvas e no primeira quadrante, ou seja, a seguinte região
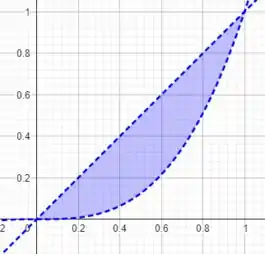
Quando temos uma integral calculada ao longo de uma curva que é fronteira orientada positivamente de uma região, isso grita para usarmos o teorema de Green, que nos diz que
Então todo o problema revolve em mudar o tipo de integração que iremos realizar! belezinha? vamos lá!
Passo 2
Observando a nossa integral, temos que
e
Calculando as derivadas parciais
lembre, que quando calculamos a derivada parcial em relação a toda função de é tomada como constante, portanto, temos que a derivada acima se reduz à
já que derivadas de constantes são . Lembrando então que pela regra do tombo, temos que
Agora, para a outra derivada parcial, temos que
note que na verdade é simplesmente , ou seja, a derivada em relação a desta função é simplesmente , temos que
e, finalmente, nossa integral irá se tornar
Ótimo! Bem mais simples não é? Agora é só determinarmos a ordem da nossa integração! E o problema já era!
Passo 3
Note que a variável varia simplesmente de até (dá uma olhada em nossa região), mas, a variável vai de até , portanto, precisamos primeiro integrar em , já que os limites são funções de , temos então que
A primeira integral pode ser identificada através de primitiva como
Usando este resultado, temos que
Ambas as integrais podem ser identificadas em termos de primitivas, temos que
ou, simplesmente
Da mesma forma, temos para a segunda integral que
avaliando os limites
Ou seja, usando ambos os resultados, temos que a nossa integral é
A questão foi isso! Te vejo na próxima! Tchau Tchau!