Questão 2) Calcule a área delimitada pela curva
Conforme a figura a seguir:
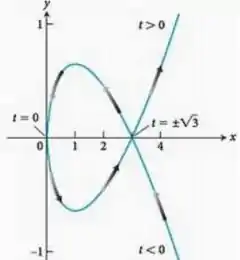
Passo 1
A área de uma região plana sempre é dada por uma integral dupla, bem famosa por sinal:
Acontece que nesta forma de calcular a área, precisamos descrever a região de alguma forma - normalmente é do tipo ou . Mas se você notar, não temos uma região muito legal, então vai ser difícil descrevê-la.
Bem, então o que fazer?
Vamos usar o que temos em mãos, a curva ;)
Passo 2
O fato de ter uma curva já parametrizada delimitando a região indica que vamos ter que utiliza-la, mas como? Bem pelo teorema de Green, temos uma relação entre a integral de linha com a dupla:
Onde é uma função vetorial com expressão...
Então repare que se fizermos...
Temos a área relacionada com uma integral de linha.
Agora a pergunta que não sequer calcular: Quem vem a ser a função ? Bem, qualquer função que satisfaça a condição dessa subtração de derivadas parciais, saca? É sempre interessante pegar:
Passo 3
Agora, não podemos sair aplicando essa igualdade entre essas integrais assim... De qualquer maneira. Temos sempre que averiguar se estamos nas condições belezinha do Teorema:
1º - deve ser uma curva fechada delimitando :
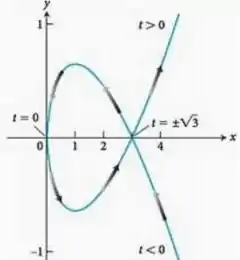
O que já temos!
2º - Ela deve estar orientada positivamente:
O que também já acontece pelo fato dela girar no sentido anti-horário.
3º - A função não pode ter singularidades:
Ora, a gente quem escolheu essa função, e a gente não ia pegar uma com fração pra correr o risco do denominador zerar em algum lugar, neh?
Passo 4
Condições satisfeitas, de fato podemos aplicar a igualdade:
Se vamos buscar a solução dessa integral de linha do modo diretão, nada mais justo que seguirmos o passo a passo maroto de resolução desse tipo de integral:
- Parametrizar a curva que estamos trabalhando
- Substituir os termos do campo vetorial pelos termos da parametrização
- Encontrar o termo
Passo 5
Deveríamos aqui parametrizar essa curva, mas para a nossa alegria... Ela já está parametrizada !
Onde varia...
Passo 6
Beleza! Agora devemos prosseguir substituindo no campo vetorial , esse e pelos termos da parametrização:
Como na parametrização que temos,, é a primeira entrada e é a segunda...
Basta substituir no campo vetorial:
Passo 7
Para encontrar o termo , basta sabermos que facilmente o encontramos fazendo:
Como no caso a parametrização foi , derivando cada termo do vetor em relação a ...
Logo...
Passo 8
Voltando para a integral de linha que estamos trabalhando
e substituir todos os dados que obtivemos...
Não se esqueça de realizar esse produto escalar de vetores aí, heim!
Agora basta que resolva a integral e correr para o abraço!