Encontre a área da superfície obtida girando-se uma curva plana em torno do eixo
Passo 1
Vamos dar uma leve manipulada nessa curva . Até então a gente tem
Isso a gente pode reescrever como
Vamos parametrizála como
Com dando a volta completinha (entre 0 e.
Passo 2
A área da superfície obtida quando giramos em torno do eixo nos é dado por
E esse , quanto que vale mesmo?
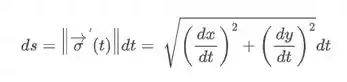
Acabou
Resposta
Exercícios de Livros Relacionados
Como se integra uma função sobre uma superfície parametrizada no espaço? E de superfícies que são definidas implicitamente ou na forma explícita? O que se pode calcular com asintegrais de superfície?
Área de uma região elíptica - Encontre a área da região elíptica cortada do plano x + y + z = 1 pelo cilindro x 2 + y 2 = 1 .
Área de uma calota parabólica - Encontre a área da calota cortada do paraboloide y 2 + z 2 = 3 z pelo plano x = 1 .
Cilindro circular cortado por planos - Integre g x , y , z = x 4 y y 2 + z 2 sobre a porção do cilindro y 2 + z 2 = 25 que está no primeiro octante entre os planos x = 0 e x = 1 e acima do plano z = 3