UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV2 - 2023.1, Questão 1
Encontre a área da calota cortada do hemisfério , pelo cilindro .
Passo 1
Olá meu amigo, tudo bem? Antes de calcularmos a área propriamente dita, é melhor primeiro olhar a forma da nossa calota, e para isso utilizaremos o GeoGebra.
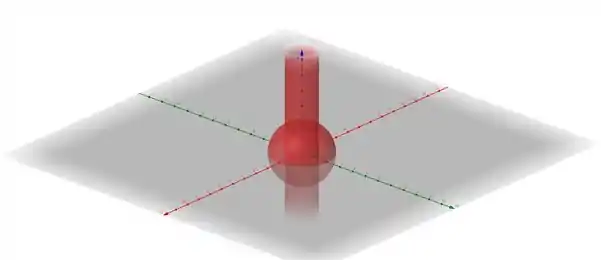
Nossa região é do círculo superior que está dentro do nosso ‘tubo’. A gente quer a área daquela casquinha de cima, pensa que é o topo brilhante de um calvo hehehe
Passo 2
Primeiro iremos manipular a expressão da esfera pra deixa-la forma . Pois assim poderemos utilizar uma formula para resolver essa integral.
Para esse caso, nossa equação que calcula a área da superfície fica
Realizando as derivadas parciais, teremos como resultado isso aqui
E
Passo 3
Desenvolvendo agora a raiz
Agora, para nossa paz e sossego iremos utilizar coordenadas polares para resolver essa querida integração, pois será bemmm mais facil para a gente. E para isso temos que,
E a nossa integral agora tem a seguinte cara
Calculando a integração mais interna
Indo para a integral mais externa
E aqui terminamos nossa querida questão, forte abraço e até uma próxima.