O bloco de está em repouso sobre a superfície horizontal e uma força , cuja direção pode ser variada, é aplicada ao bloco.
- Calcule o coeficiente de atrito estático , entre o bloco e a superfície, se o bloco começa a deslizar quando é reduzido para
- Se é aplicado com , calcule a força de atrito
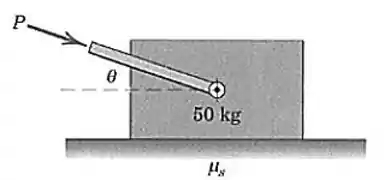
Passo 1
Quando aplicamos a força surge uma força de atrito contrária ao movimento:
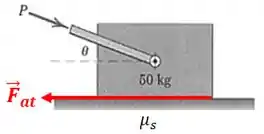
O módulo da força de atrito é dado por:
Onde é o módulo da força normal.
Passo 2
Bom, para que o bloco esteja em equilíbrio, precisamos satisfazer as seguintes condições:
Temos essas forças atuando no bloco:
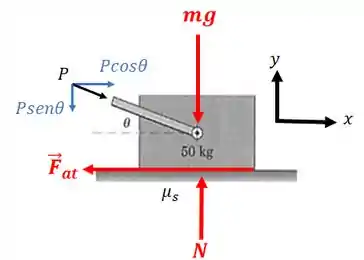
Repare que para achar as componentes verticais e horizontais da força temos que fazer:
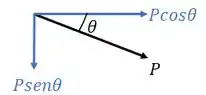
Então, fazendo o equilíbrio das forças horizontais vamos ter que:
Show de bola! Já achamos uma relação para achar Basta a gente calcular o módulo da força normal agora fazendo o equilíbrio de forças verticais:
Lembrando que , vamos ter que:
Agora podemos calcular :
Passo 3
Agora temos que calcular a força de atrito para . Para isso vamos fazer o equilíbrio horizontal: