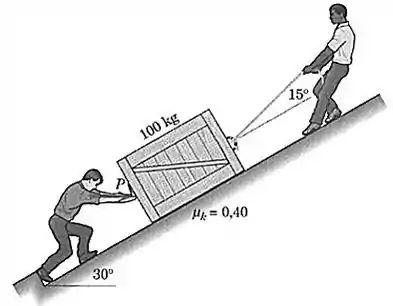
Dois homens estão deslizando um caixote de para cima no plano inclinado. Se o homem de baixo empurra horizontalmente com uma força de e se o coeficiente de atrito dinâmico vale , determine a força trativa que o homem de cima deve exercer na corda para manter o movimento do caixote.
Passo 1
Vamos começar fazendo o diagrama de corpo livre do caixote:
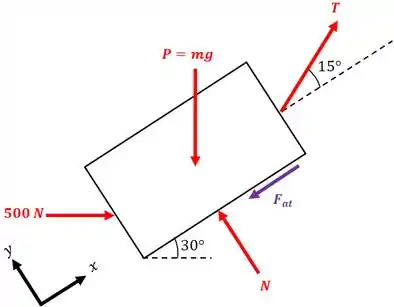
Repare que a força de é horizontal, pois foi dito isso no enunciado.
Como o bloco está se movendo, estamos lidando com o atrito dinâmico, o qual pode ser calculado pela seguinte fórmula:
Então, a nossa força de atrito será:
Como ainda não sabemos o valor da normal, vamos deixar assim!
Passo 2
Vamos começar fazendo o equilíbrio das forças que estão na direção do eixo . Para isso, precisamos decompor algumas das forças. Vamos começar pela força peso:
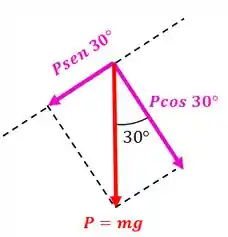
O módulo da força peso vale:
Já as componentes da força de vão ficar assim:
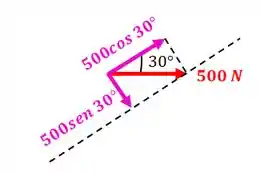
E por fim a força trativa :
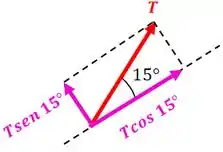
Beleza?
Agora sim podemos fazer o somatório das forças na direção :
Vamos guardar esta equação!
Agora vamos fazer o equilíbrio de forças na direção :
Passo 3
Agora temos duas equações e duas incógnitas. Vamos resolver o sistema:
Vamos isolar a normal da segunda equação:
E substituir isso na primeira equação:
Agora que sabemos o valor de , podemos achar quanto vale a normal: