Determine o módulo e a direção da força de atrito que a parede vertical exerce sobre o bloco de se:

Passo 1
As forças que agem nesse sistema são: a força peso (), a força de atrito (), a força normal () e a força
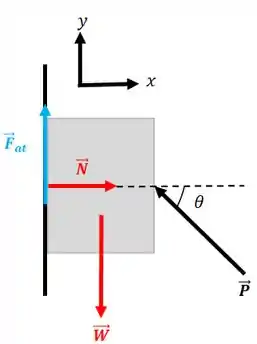
Perceba que a normal é horizontal, porque ela surge do contato entre o bloco e a parede.
E arbitramos o atrito apontando para cima, quando fizermos o equilíbrio veremos se acertamos ou não dependendo do sinal que encontrarmos para a .
Passo 2
Vamos ao primeiro caso, quando o ângulo vale Vamos começar pelo equilíbrio vertical:
Perceba que temos que decompor a força no eixo :
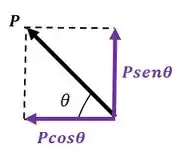
Então, vamos ter que:
Perceba que a deu positiva, isso significa que ela realmente aponta para cima!!!
Nós achamos o módulo da força de atrito....mas será que ela vale isso mesmo?
O que precisamos fazer é verificar se essa força está no atrito estático ou dinâmico.
Para isso, vamos calcular o atrito estático máximo. Se a nossa for menor que o valor máximo, ela estará correta. Se ela for maior, significa que o valor da força entrou no regime dinâmico. Daí teremos que calcular o atrito dinâmico, que é constante.
Para achar o atrito estático máximo, usamos:
Quanto vale a normal? Vamos descobrir isso fazendo o equilíbrio das forças horizontais:
Assim, o atrito máximo estático vale:
Perceba que o atrito que achamos é maior que o atrito estático máximo:
Sendo assim, o atrito é dinâmico. Então, temos que calcular o atrito utilizando a fórmula de atrito dinâmico:
Passo 3
Agora faremos a mesma coisa, só que com . Então, vamos começar pelo equilíbrio das forças verticais:
Vamos calcular o valor da normal nesta situação fazendo o equilíbrio das forças horizontais:
Agora podemos calcular a força de atrito estático máximo:
Perceba que o atrito que achamos é menor que o atrito estático máximo:
Então, a nossa força de atrito está correta: