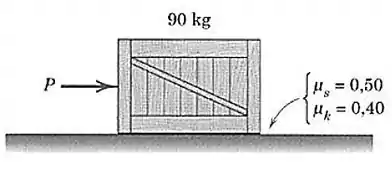
A força é aplicada ao caixote de , que está em repouso antes que ela seja aplicada. Determine o módulo e a direção da força de atrito exercida pela superfície horizontal sobre o caixote se:
- ;
- ;
- .
Passo 1
Podemos representar o nosso caixote assim:
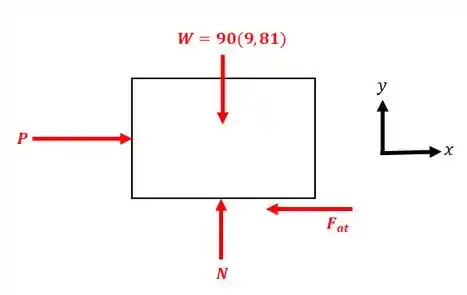
Repare que ao aplicar a força surge uma força de atrito contrária à tendência de movimento, ou seja, apontando para o sentido negativo do eixo .
O módulo da força de atrito é dado por:
Onde é o módulo da força normal.
Passo 2
Bom, para que o bloco esteja em equilíbrio, precisamos satisfazer as seguintes condições:
Então:
E na vertical vamos ter que:
Passo 3
Com esse valor da força normal, podemos calcular a força de atrito máxima para que o bloco continue parado:
Sabendo que , vamos analisar cada situação:
- :
- :
- :
Neste caso, a força é menor do que a máxima força de atrito que pode ter para que o bloco continue parado, então o caixote não irá se mover:
Neste caso, a força continua menor do que a máxima força de atrito que pode ter para que o bloco continue parado, então o caixote também não irá se mover:
Neste caso, a força ultrapassou a máxima força de atrito que pode ter para que o bloco continue parado, então o caixote deixa de ter uma força de atrito estática e passa a ter uma força de atrito dinâmica, que é dada pela expressão: