02) Considere o sistema em equilíbrio mostrado na figura. A barra homogênea AB tem peso e está apoiada na superfície horizontal em A, com atrito, cujo coeficiente é , desconhecido. A barra BC tem peso desprezível e possui articulações ideais em ambas as extremidades. Responda o que é solicitado abaixo, preenchendo os respectivos campos sem incluir unidades.
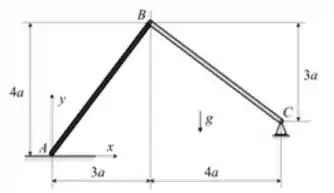
a) Calcular o módulo da força na barra BC.
b) Determinar se a força na barra BC é de tração ou de compressão.
c) Calcular o módulo da força de atrito em A na barra AB.
d) Calcular o menor coeficiente de atrito entre a barra AB e a superfície horizontal que seja compatível com o equilíbrio estático.
Passo 1
Eaí gente, vamo detonar mais uma questão de mecânica!
a) Nesse exercício temos duas barras ligadas e apoiadas em um lado numa superfície rugosa, e no outro, em uma articulação. Ao longo dos itens deveremos encontrar as forças que agem nas barras e a força de atrito.
Por isso, a melhor forma de atacar essa questão é desenhar os diagramas de corpo livre (DCL), escrever as equações de equilíbrio e partir pras contas.

Então beleza! Pensando no DCL da barra BC, basicamente as forças que atuam nela são devidas às articulações em B e C. Barras de treliça devem ter força atuando na direção do próprio eixo da barra, assim, supondo que elas estejam comprimidas, temos:
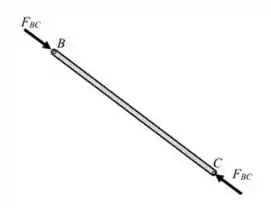
Massa! Já pra barra AB vamos ter mais forças atuando. Começando pelo ponto B, temos a reação da força atuando em B. Além disso, temos a força peso atuando no meio da barra, além do atrito e da normal em A. Daí a gente pode desenhar também o DCL de AB:
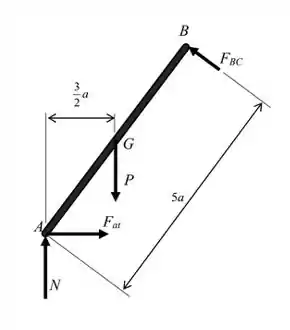
Beleza galera, agora que já temos o DCL da barra AB podemos tirar as equações do equilíbrio estático:
Passo 2
b) Olha aí, naturalmente achamos . Como encontramos um resultado positivo, significa que o sentido suposto está correto, ou seja, BC está sendo comprimida.
Passo 3
c) Vamos continuar e escrever as equações de equilíbrio restantes:
Agora para resultante no eixo nula, temos:
Muito bom! Já vamos pro próximo item então.
Passo 4
d) Aqui precisamos calcular o coeficiente de atrito mínimo para garantir o equilíbrio estático.
A ideia é sempre lembrar que a força de atrito não tem uma fórmula específica pra determiná-la, mas vale sempre que:
Logo, o valor mínimo ocorre na igualdade. Pelos resultados do item anterior, teremos:
Prontinho! É importante demais conhecer e saber usar essa desigualdade da força de atrito.
Valeu pessoal, espero que vocês tenham entendido bem! Tamo junto 😊
Resposta
a)
b) Compressão.
c)
d)