Um bloco de massa é colocado entre a parede vertical e o pequeno rolete ideal da extremidade superior, , da barra esbelta uniforme de massa A extremidade inferior, , da barra repousa sobre a superfície horizontal. Se o coeficiente de atrito estático em e também entre o bloco e a parede vale , determine a expressão geral para o valor mínimo , de para o qual o bloco permanecerá em equilíbrio. Avalie sua expressão para e . Para essas condições, verifique a possibilidade de haver deslizamento em
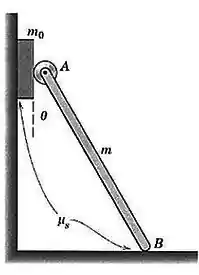
Passo 1
Nosso primeiro passo é montar o diagrama de corpo livre:
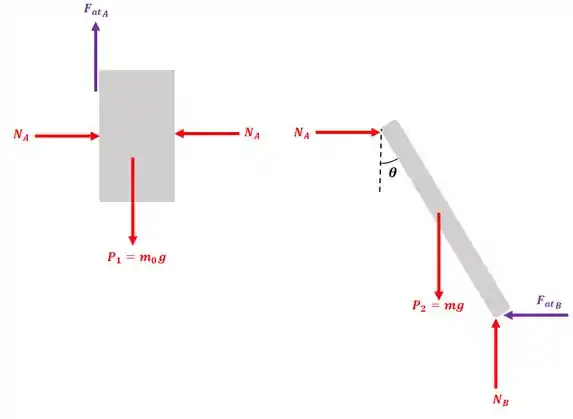
Passo 2
Vamos analisar primeiro o nosso bloco:
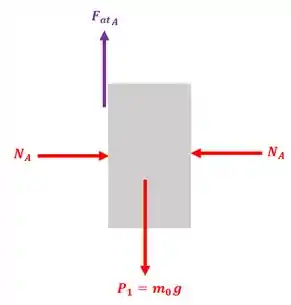
Perceba que só existe atrito no lado esquerdo do bloco, ou seja, atrito entre o bloco e a parede. Isso acontece porque no lado direito tem um rolete ideal, ou seja, sem atrito.
Como estamos lidando com uma situação extrema, devemos calcular o atrito como sendo o máximo. Então, o atrito entre o bloquinho e a parede será:
Vamos achar a normal no ponto fazendo o equilíbrio das forças verticais que atuam somente no bloquinho:
Passo 3
Agora vamos analisar a barra...
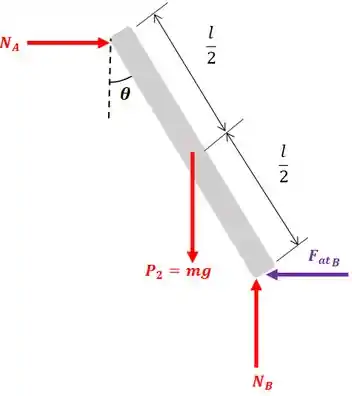
Onde é força de atrito em .
Vamos agora calcular, através do equilíbrio de momentos, outro valor para . Para isso, vamos fazer o somatório de momentos em relação à (isso elimina as forças e
Repare que distância da força peso da barra até o ponto é:
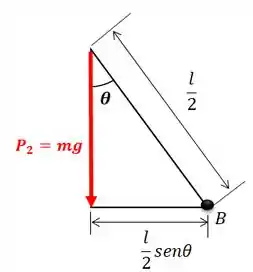
E a distância da força normal até o ponto é:
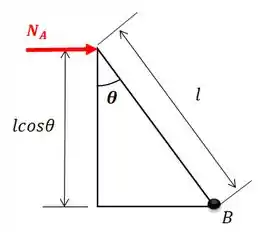
Então, considerando o momento positivo girando no sentido horário, o somatório de momentos com relação ao ponto das forças que atuam somente na barra fica assim:
Então, a força normal que atua na barra é:
Passo 4
Mas perceba que a força normal do bloco é transmitida para a barra por causa do contato entre esses dois elementos:
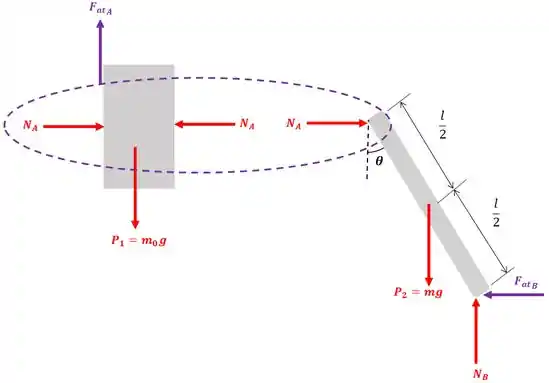
Ou seja, vamos igualar as duas expressões que achamos para :
Como queremos saber , vamos isolar o ângulo na expressão acima:
Perceba que estamos partindo do princípio que tudo está em equilíbrio. Assim, esse é o ângulo mínimo que estávamos procurando.
Sabendo que e , vamos ter que:
Passo 5
Agora precisamos verificar se esse ângulo realmente mantém o conjunto em equilíbrio...
Para isso, vamos checar se a força de atrito em é menor que a força de atrito máxima. Se for menor, isso significa que o ponto não entrou no regime dinâmico o que, em outras palavras, quer dizer que a barra não começou a deslizar.
Então, vamos fazer o equilíbrio horizontal das forças:
Mas sabemos que para a barra:
Então vamos substituir isso na nossa equação de equilíbrio:
Mas sabemos que , então:
Agora vamos fazer o somatório das for��as verticais para acharmos a força normal em :
Com , podemos calcular a força de atrito máxima:
Agora temos que comparar a força de atrito em que achamos com o seu valor máximo para que a barra continue parada:
Ou seja, o valor que achamos realmente é menor do que o valor máximo. Então, podemos garantir que a barra realmente não irá deslizar!