03) As massas das caixas mostradas na figura valem e , e o coeficiente de atrito estático entre todas as superfícies em contato vale .
Considerando , calcule a menor força que deve ser aplicada para que o conjunto não deslize.
Na resolução devem constar os DCL’s e as equações de equilíbrio necessários à resolução do problema.
Passo 1
Faaala galera, tudo certinho com vocês?
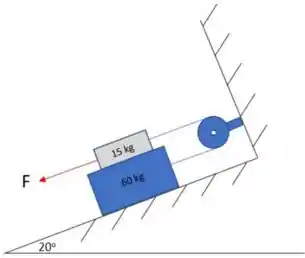
Nessa questão temos um plano inclinado de , onde dois blocos empilhados (um de e outro de ) estão apoiados com . Ambos os blocos estão ligados por um fio tracionado que passa por uma polia.
O objetivo é determinar a menor força que deve ser aplicada no bloco de para que todo o conjunto não deslize. Beleza?

Massa! Um primeiro passo bem importante nesse tipo de questão é determinar as equações de equilíbrio, e pra fazer isso é uma ótima ideia desenharmos o diagrama de corpo livre (DCL) dos dois blocos.
Bora lá!
Passo 2
Começando pelo bloco de , atua sobre ele a força , o peso com suas componentes, a normal de contato, a força de tração e o atrito entre os blocos.
Mas, qual que vai ser o sentido do atrito se queremos calcular a menor força ?

Pensa comigo, se queremos a menor força pra deixar o conjunto em equilíbrio, vai apenas impedir a tendência natural de movimento do conjunto. Ou seja, vai impedir que o bloco mais pesado desça o plano inclinado e que o mais leve suba.

Daí, o atrito atuando no bloco de deve estar em sentido contrário à sua subida, conseguiu pegar a ideia?!
Desenhando o DCL, vamos ter:
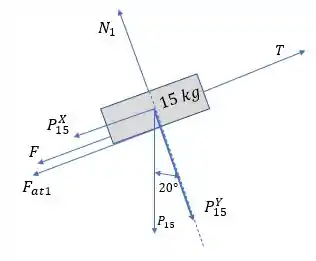
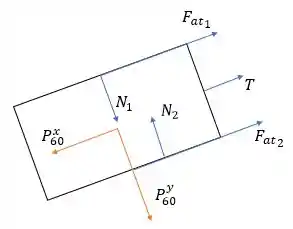
Show! Já para o bloco de vamos ter o peso (com suas componentes), a normal de contato com a superfície do plano e também entre os blocos, a tração , o atrito entre os blocos e também com a superfície inclinada. Puts, é muita força né...

O atrito entre os blocos deve ter sentido oposto ao desenhado no DCL anterior, já o atrito com a superfície inclinada tem sentido oposto à descida do plano inclinado (pois esse é o movimento que o bloco de tenta fazer). Assim, podemos desenhar:
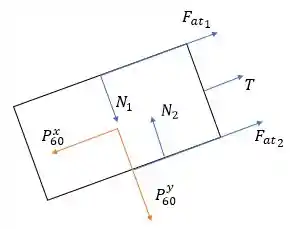
Muito bom!
Passo 3
Agora que já temos os DCL’s podemos escrever a 2° lei de Newton para os blocos.
Sendo o eixo perpendicular à superfície inclinada, e a tangencial, para o bloco de podemos escrever:
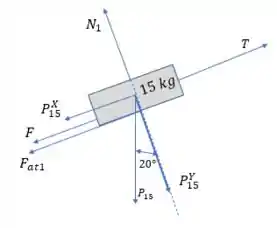
Onde é a massa do bloco de .
Daí, substituindo o valor de na equação em temos:
Top! Pensando agora no nosso bloco de , também podemos escrever a lei de Newton pra ele. Daí, vem:
onde é a massa do bloco de .
Substituindo na equação em , e sabendo também que , temos:
Perfeito!
Agora é só manipulação algébrica.

Igualando e vem que:
Aí é só isolar e partir pras continhas:
Como e, vem:
Fazendo essas continhas de cabeça (só que não haha), finalmente chegamos que:
Prontinho! Matamos mais uma questão galerinha!
Espero que vocês tenham curtido a solução, até a próxima 😉