2) A estrutura ilustrada na figura é constituída pelas barras articuladas e , ambas de peso desprezível. Em há uma polia, também de peso desprezível, que sustenta uma carga de peso P por meio de um cabo inextensível ideal. A extremidade A da barra AC apoia-se em uma parede vertical, e o coeficiente de atrito estático no contato entre a parede e a barra é . Todos os vínculos são ideais e o sistema está em equilíbrio. Admitindo , calcule e escreva suas respostas nos campos abaixo. Responda o que é solicitado abaixo, preenchendo os respectivos campos sem incluir unidades e com apenas 2 casas decimais. Utilizar PONTO como separador de decimais.

a) A força de tração no cabo.

b) Os módulos das componentes da força em D.

c) Os módulos das componentes da força em A.

d) O menor coeficiente de atrito entre a barra AC e a parede vertical que seja compatível com o equilíbrio estativo da estrutura.

b)Bom, agora a questão nos pede para determinar o módulo das componentes da força em D. Como temos uma barra e uma polia articulada em D, devemos ter forças de reação nesse ponto. Tanto uma reação vertical , como uma reação horizontal .

Uma boa ideia para descobrir esses caras é justamente desenharmos o diagrama de corpo livre da nossa polia e analisarmos o seu equilíbrio.

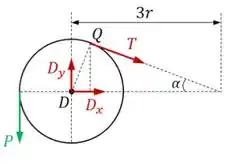
Beleza, vamos agora montar as equações de equilíbrio das forças. Temos que:

Precisamos encontrar o valor do seno e cosseno de . Usando a geometria do problema e o teorema de Pitágoras, podemos montar o seguinte triângulo:

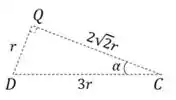
Daí vem que:

Das equações de equilíbrio, podemos escrever que:

Como , podemos concluir mais um item com:

Aee, aos pouquinhos tamo matando a questão. Vamos lá!

c)

Nesse item precisamos calcular o módulo das componentes das forças em . A ideia é que como a barra está encostada na parede numa situação de equilíbrio estático, deve haver reação da parede na barra para conseguir manter esse equilíbrio.

Para conseguir extrair as equações de equilíbrio, vamos desenhar o diagrama de corpo livre das barras. Lembrando que as forças e deverão estar no sentido oposto ao do diagrama da polia, pois o ponto D precisa estar em equilíbrio também.

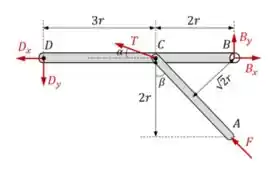
Aqui temos que ser espertos. Podemos ter um trabalho muito grande escrevendo todas as equações de equilíbrio (tanto de força como de momento) para esse conjunto de barras, ou podemos pensar em apenas uma equação de equilíbrio que nos permita encontrar logo o valor de .

Conseguiu descobrir? É justamente a equação do momento em relação a B. Como as variáveis e não são pedidas na nossa questão, eliminamos essas variáveis da nossa conta calculando o momento em B, já que uma força não faz momento no próprio ponto em que está atuando. Daí:

Substituindo os valores de e T encontrados nos itens a e b, ficamos com:

Beleza! Mas lembra que o que a questão nos pede são as componentes da força em A, então analisando melhor as forças no ponto A temos:

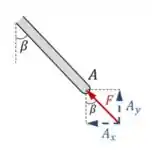
Assim, vale que:

E:

Mas, olhando pra figura do DCL das barras, vemos que , pois os catetos são iguais a . Logo,

Perfeito!! Vamos ter então que:

Prontinho 😊

d)

Esse item é bem legal. A ideia aqui é que, na realidade, o que temos chamado de é justamente a força de atrito entre a parede e a barra . Assim, como a força de atrito é no máximo igual a força de atrito estática, podemos escrever que:

Só que a normal da barra na parede é justamente a reação Daí:

Portanto, concluímos que o menor valor possível do coeficiente de atrito vale:

Boaa, matamos mais uma questão de mecânica e trabalhamos vários conceitos legais. Bora pra próxima, aprender mais um pouco 😉