A roda mostrada rolará para a esquerda quando o ângulo do cabo for pequeno. Quando for grande, a roda rolará para a direita. Determine, por inspeção da geometria do diagrama de corpo livre, o ângulo para o qual a roda não rolará. Se o coeficiente de atrito estático e a massa da roda é , determine o valor de para o qual a roda girará para o valor crítico de
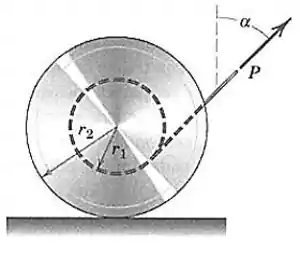
Passo 1
Pense o seguinte: quando a roda não gira, o momento resultante é nulo, certo? Vamos pensar no ponto de giração abaixo, logo onde existe o contato entre a roda e o chão:
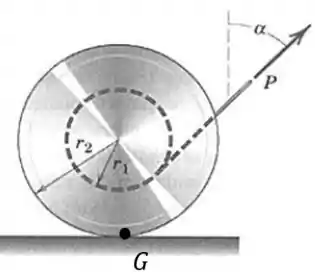
Se o momento resultante em relação a esse ponto for nulo, não ocorrerá o giro. E como garantimos isso?
Simples, basta que todas as forças sejam concorrentes nesse ponto, ou seja, que a linha de ação das forças que atuam na roda passe por este ponto. Sabemos que a força normal e o peso passam pelo ponto , só falta saber a força
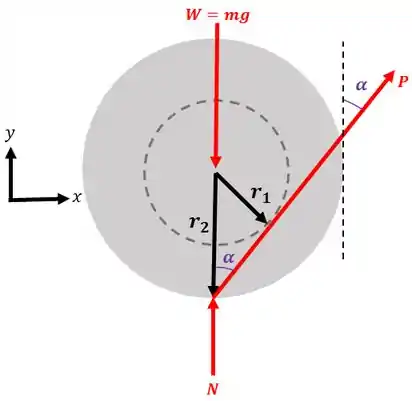
Precisamos fazer a força passar pelo ponto de contato entre a roda e o chão, porque assim ela não gera momento com relação a este ponto (já que não vai ter braço de alavanca). Observe que o peso e a força normal passam por esse ponto.
Temos que arranjar um jeito de colocar o ângulo em função dos nossos dados que são os raios e . Para isso, vamos usar esse triângulo retângulo aqui:
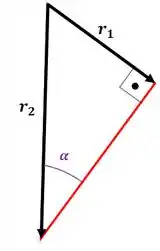
Então, podemos dizer que:
Beleza?
Passo 2
Agora vamos utilizar as equações de equilíbrio para fazer achar a normal e a força de atrito. Para isso temos que achar as componentes vertical e horizontal da força :
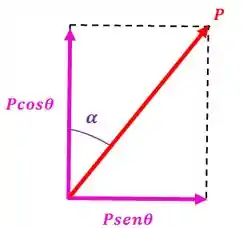
Vamos começar fazendo o somatório das forças verticais:
E o equilíbrio horizontal fica:
Passo 3
Como queremos saber o ângulo máximo para o qual a roda não irá girar, ela estará na parte do atrito estático. Então, temos que calcular o atrito estático máximo:
Então, a nossa equação do equilíbrio horizontal pode ser escrita assim:
Mas já temos uma expressão para a força normal, lembra?
Vamos substituir ela na equação do equilíbrio horizontal:
Como queremos saber , vamos isolá-lo na equação:
Beleza?
Passo 4
Ainda temos que ajeitar mais a expressão de ...
Nós sabemos que:
Lembra da fórmula fundamental da trigonometria? Ela diz que:
Então, para saber quanto vale o vamos fazer:
Podemos ajeitar melhor isso:
Agora é só substituirmos o e o na nossa equação para achar :
Agora vamos arrumar essa expressão aí: