A força é aplicada ao caixote de quando ele está em repouso. Determine o módulo e a direção da força de atrito exercida pela superfície sobre o caixote se
Que valor de é necessário para iniciar o movimento para cima do plano inclinado? Os coeficientes de atrito estático e dinâmico entre o caixote e o plano são e , respectivamente.
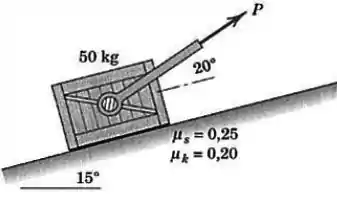
Passo 1
Nesse caso, como , estamos lidando com um problema de plano inclinado onde só temos a força peso () do bloquinho e a normal que surge do contato entre o bloco e a superfície:
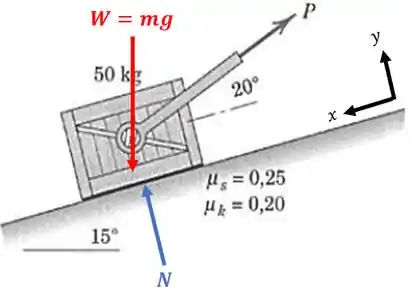
Vamos decompor a força peso no eixo :
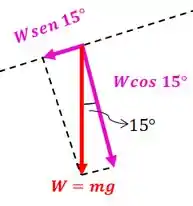
Nesse caso, as componentes do peso ao longo do plano e perpendicular ao mesmo são:
Onde é o peso do bloquinho e vale:
Passo 2
Quando o bloquinho tende a descer o plano inclinado, surge uma força de atrito contrária ao movimento:
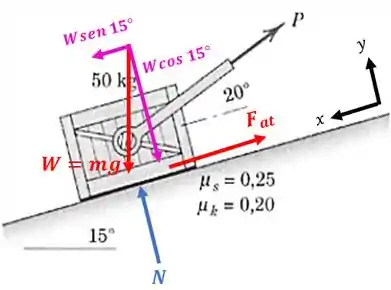
Vamos fazer o equilíbrio das forças que estão no eixo :
Duas forças agem ao longo do plano: a força de atrito e a componente do peso. Assim:
E ao longo do eixo Nesse caso, existe a força normal e a componente do peso:
E agora? O que temos que fazer? Temos que ver se aquela força de atrito não ultrapassa o atrito estático máximo. Caso ultrapasse, o atrito que estamos lidando é o dinâmico e teremos que recalcular.
Então:
Perceba que o atrito que achamos é maior que o atrito máximo:
Então, o atrito, na verdade, é dinâmico e deve ser calculado pela fórmula do atrito dinâmico:
E a sua direção e sentido? A força de atrito é contrária ao movimento do bloquinho, então ela aponta no sentido da parte negativa do eixo
Passo 3
Agora vamos considerar a força . Vamos fazer quase a mesma coisa, só que agora vamos incluir nas equações as componentes da força
Então vamos decompor esta força no nosso eixo :
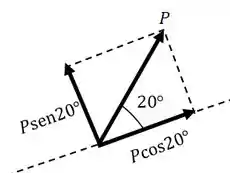
Então, fazendo o equilíbrio das forças que estão no eixo , temos:
Opa, o atrito deu negativo. Isso quer dizer que assumimos um sentido errado para o atrito. Se você reparar na nossa equação acima, assumimos que ele aponta no sentido contrário ao eixo . Como o sinal deu negativo, ele aponta no sentido positivo do eixo :
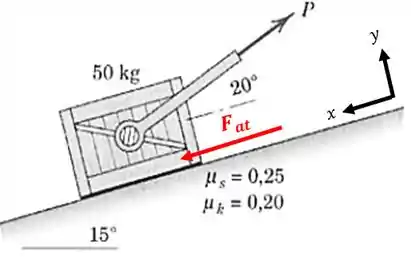
Então, o vetor da força de atrito fica assim:
E agora? Agora a gente tem que ver se o valor da força de atrito que calculamos é maior ou menor que a força de atrito máxima.
Para isso temos que calcular a normal novamente fazendo o equilíbrio das forças que estão no eixo :
Agora vamos calcular a força de atrito estático máxima:
Perceba que a força de atrito que calculamos é menor que a força de atrito estático máxima!
Então, a nossa premissa de que a força de atrito era menor que a for��a de atrito máxima estava correta e podemos dizer que:
Passo 4
Agora vamos considerar a força .
Vamos fazer a mesma coisa que antes, só mudamos o valor da força. Assim:
Se deu negativo, então o sentido que escolhemos para a força de atrito estava errada. Como estávamos assumindo que o atrito apontava para cima, ele na verdade está apontando para baixo:
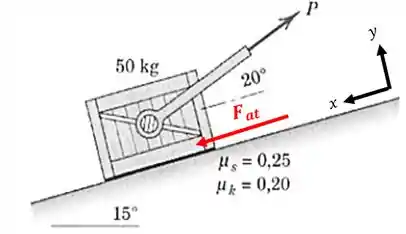
Então, a força de atrito pode ser escrita assim:
Mas precisamos calcular a força de atrito estático máxima novamente, pois o valor da normal vai mudar. Então, vamos fazer o equilíbrio das forças que estão no eixo :
Então, a força de atrito estático máxima vai ser:
Perceba que a força de atrito que achamos é maior que a força de atrito estático máxima:
O nosso atrito é, na verdade, dinâmico. Então, precisamos usar a fórmula do atrito dinâmico para calculá-lo:
Então, o nosso atrito é:
Passo 5
O valor de necessário para iniciar o movimento para cima do plano inclinado é tal que a componente de no eixo esteja prestes a superar o valor máximo do atrito estático menos a componente do peso do bloco que está no eixo :
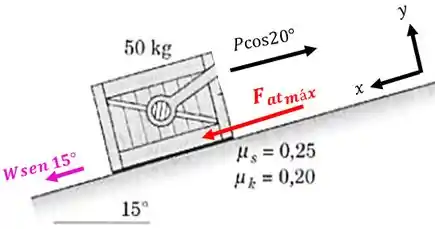
Isso significa que para se iniciar o movimento:
Vamos considerar a situação do “prestes a superar”, igual a:
Neste caso:
O é ângulo de inclinação da força que é de . Vamos deixar para substituir seu valor lá no final!
Mas o valor de é estabelecido através da equação de equilíbrio no eixo :
Substituindo na primeira equação que achamos, vamos ter que:
Substituindo os valores, encontramos: