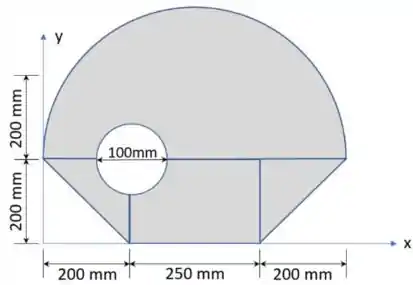
02) Calcule a coordenada do centroide da figura abaixo:
Passo 1
Eaí galerinha! Como vocês estão?
Nessa questão nos é pedido para calcular a coordenada do centroide, ou seja, o centro geométrico de uma área plana.
O que é importante a gente perceber é justamente o formato dessa área, que não é uma figura geométrica simples. Nesses casos, a principal ideia que usamos é um raciocínio pelo princípio da superposição, tentando gerar essa área através de áreas conhecidas, como círculos, semicírculos, triângulos e retângulos.
Então bora fazer isso fechando esses triângulos debaixo, como também o semicírculo.
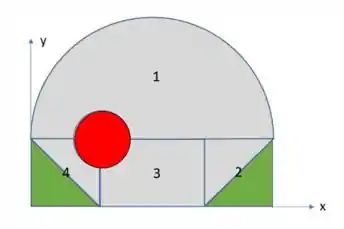
Observando a figura acima, conseguimos perceber os dois triângulos verdes e círculo vermelho que adicionamos. Isso foi muito bom, porque agora temos apenas figuras geométricas que conhecemos os respectivos centroides.
Passo 2
Beleza! Vamos então calcular qual seria o centroide dessa figura que geramos completando a imagem do enunciado. A ideia é fazer:
Vamos calcular separadamente cada um desses termos:
- Figura 1:
De resultados já conhecidos (que para esse caso clássico vale a pena decorar, pois não é tão simples, temos que a coordenada do centroide de um semicírculo, vale:
O raio pode ser calculado como metade do diâmetro, que pode ser visto na figura do enunciado como:
Levando em consideração a origem do nosso plano cartesiano, bem como o valor do raio desse semicírculo, temos que:
Já a área 1, é a área de um semicírculo. Logo:
Excelente, bora pra próxima.
- Figura 2:
Aqui temos um quadrado. A posição do seu centroide é bem conhecida né galera? O centro geométrico de um quadrado obedece à simetria, logo:
Massa. Já a sua área vale:
- Figura 3:
Nesse caso, temos um retângulo, cujo centroide também se encontra na meta da sua altura. Logo:
Já para o cálculo da sua área, temos:
- Figura 4:
Por último, mas não menos importante, precisamos calcular e . O legal é que essa figura é idêntica à figura 2, assim:
Por último:
Beleza, agora é só substituir na nossa expressão pro CG, daí fica:
Aee, conseguimos determinar o centro geométrico dessa figura mais completa.
Passo 3
Pra conseguir calcular o da figura do enunciado podemos usar o princípio da superposição, fazendo algo tipo isso:
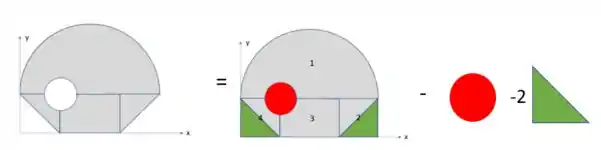
Mas para os valores dos produtos de cada uma dessas figuras.
Para o primeiro termo, já calculamos e encontramos:
Já o do círculo está bem no centro dele, considerando o nosso plano cartesiano, temos:
Por último, para o triângulo o CG se localiza no baricentro, que vai estar a uma altura do lado base. Logo:
Prontoo, podemos escrever então que:
Por fim, nós finalmente encontramos que:
Ufa, matamos mais uma. Essa questão foi bem interessante né? Trabalhou bem os conceitos de centroide e também a ideia do princípio da superposição. Espero que vocês tenham entendido direitinho, até a próxima pessoal!!!