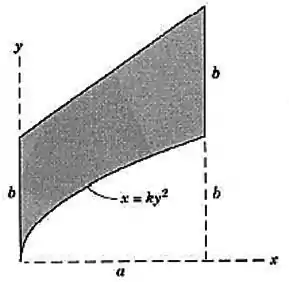
Determine a coordenada do centroide da área sombreada.
Passo 1
Vamos começar definindo as funções:
Para temos que, então:
Substituindo o valor de na equação da curva, vamos ter que:
Isolando , vamos ter que:
A outra função é uma reta:
Para temos que , então:
Para temos que , então:
Então ficamos com:
Passo 2
A área será dada por:
Repare que o elemento é dada pela diferença entre as duas funções, assim:
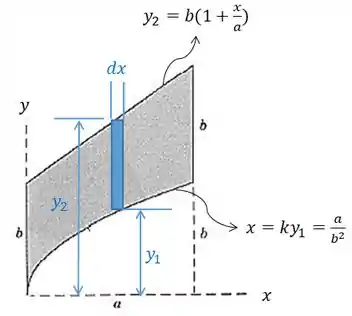
Então:
Passo 3
Agora vamos calcular a coordenada de :
Como já calculamos a área, vamos calcular agora o termo :
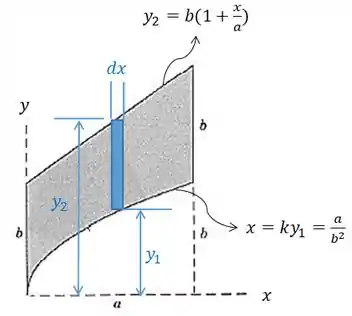
Pra calcular o que aparece dentro da integral, temos que usar sempre o , que é a média entre as funções:
Sabendo que , temos que:
Resolvendo esta integral, temos::
Então, a coordenada é:
Resposta
Exercícios de Livros Relacionados
Calcule o centroide da área abaixo em termos das variáveis dos raios:
A barra esbelta homogênea tem uma seção transversal uniforme e está dobrada na forma mostrada. Calcule a coordenada y do centro de massa da barra. (Lembrete: O comprimento do arco diferencial é d L =
Determine a coordenada z do centroide do volume obtido pela revolução da área triangular sombreada de 360° em torno do eixo z.
Localize o centro de massa do corpo sólido homogêneo cujo volume é determinado pela revolução da área sombreada de 360° em torno do eixo z.
Specify the x-, y-, and z-coordinates of the mass center of the homogeneous semicylinder.