Exercícios Resolvidos de Centros e Centróides

Enunciado

USP, Mecânica, P1-2020.2, Questão 01

01) No sistema em equilíbrio mostrado na figura, a placa homogênea OABCD, de massa , está no plano e tem seu movimento restrito pelos anéis nos pontos O e A, e pela articulação em D que une a placa às barras ED e HD. A barra ED é paralela ao eixo e a barra HD é paralela ao eixo . Ambas as barras têm comprimento e peso desprezível. Sobre a placa atuam a força e o peso . Determinar:

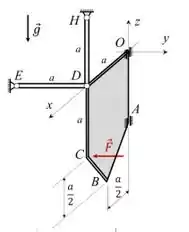
a) As coordenadas do centro de massa G da placa no sistema .

b) O diagrama de corpo livre da placa.

c) As equações de equilíbrio da placa.

d) Os esforços atuantes na barra ED.

e) As reações vinculares nos pontos e .

Passo 1

Faaala galerinha, tudo certo com vocês?

a) Pra começar mais uma questãozinha de mecânica, precisamos determinar a coordenada do centro de massa G da nossa plaquinha. Mesmo que não houvesse um item pedindo explicitamente o CM, esse passo é bem importante pra gente saber onde que atua a força peso.

Beleza, e como a gente faz isso?

O segredo, basicamente é lembrar da equação do centro de massa. Em , por exemplo:

Como a placa é homogênea, essa equação se reduz a:

Além disso, lembrar de separar a placa em figuras geométricas conhecidas (retângulos, quadrados, triângulos, circunferências).

Top, vamos então separar a nossa plaquinha em um quadrado (OACD) e em um triângulo (ABC):

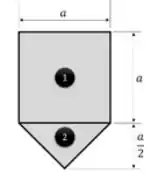
Como a parte 1 é um quadrado, pela simetria sabemos que:

Cuja área vale:

Já para a figura 2, como trata-se de um triângulo que é simétrico em relação à reta , temos:

Também, como o baricentro fica a uma distância de da altura relativa a AC, temos:

E com área:

Excelente! Agora que já determinamos é só substituir na nossa equação do centro de massa. Ficamos com:

Para terminar, como trata-se de uma placa plana em , vale que .

Prontinho! Temos que:

Passo 2

b) Aqui precisamos desenhar o diagrama de corpo livre (DCL) da placa. O problema é que além das forças já faladas no enunciado, também temos as reações dos apoios (articulação em D e anéis em O e A).

Em D, temos duas barras presas a essa articulação. Na prática é como se cada uma delas estivessem puxando (ou empurrando) o ponto D.

Já nos anéis, por se tratar de um apoio do 2° gênero, vamos ter duas forças de reação sendo geradas: uma em e outra em .

Massa! Supondo um sentido inicial para essas forças, podemos desenhar o seguinte DCL:

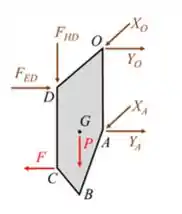
Passo 3

c) Nesse item devemos escrever as equações de equilíbrio da placa, mas que equações são essas?

Primeiro galera, se a placa está em equilíbrio é porque tanto a resultante de forças, como a resultante dos momentos em relação qualquer ponto, por exemplo, são nulas. Daí, como temos três eixos, podemos escrever a equação de equilíbrio para cada um deles:

Prontinho 😊

Passo 4

d) Aqui devemos calcular os esforços atuantes na barra ED. No caso, a barra ED se conecta à placa através da articulação em D, e nós já calculamos a reação que a barra faz em D, . Logo, pela lei da ação e reação, o ponto D faz uma força de igual intensidade, , mas de sentido oposto na barra ED.

Do equilíbrio , podemos escrever que:

Como está no sentido oposto ao do DCL desenhado no item b, temos:

(compressão)

Muito bom! Bora pro último item!

Passo 5

e) Nesse item o enunciado nos pede para calcular as reações vinculares em e , ou seja, as reações de apoio. Basicamente é olhar o sistema linear formado pelas equações de equilíbrio do item c, e meter conta Rs.

Então bora lá! De , considerando também o resultado do item anterior, temos: