02) O sistema ilustrado na figura abaixo é constituído por uma placa homogênea , de massa , e por uma barra , de massa desprezível. A placa é articulada à barra em , sendo ligada a uma parede plana vertical (plano ) por meio de uma articulação em e um anel em . A barra pertence ao plano e é ligada à parede vertical por meio de uma articulação em . Pede-se:
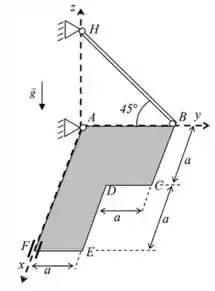
a) determinar a posição do centro de massa da placa
b) desenhar os diagramas de corpo livre da placa e da barra;
c) calcular as reações na articulação e no anel ;
d) calcular as forças na barra .
Passo 1
E aí gente, tudo certinho com vocês?
Nessa questão temos um sistema em equilíbrio estático, composto por uma placa e uma barra, que se ligam a duas articulações.
a) Pra começar, devemos determinar a posição do centro de massa da placa .
O problema é que nossa plaquinha não é uma figura geométrica clássica, que conhecemos o centro geométrico loro de cara, como um quadrado, círculo, triângulo. Então, o que podemos fazer?

A ideia é imaginarmos a placa como a superposição de duas figuras:
Um quadrado de lado e densidade igual a da placa
Um quadrado de lado e densidade negativa.
Assim, temos que:
Sacou?!
Agora é só calcular esses termos.
Como a figura é um retângulo, temos o centro de massa no seu centro geométrico. Logo:
Já para a figura , temos a densidade negativa. Assim:
Além disso, a área da placa vale:
Substituindo na nossa equação, tanto para como para , temos:
Massa! Agora para , vem:
Boua!! E , o que dá pra afirmar?
Bom, poderíamos usar a mesma equação, mas não é necessário. Como a placa está toda no plano , podemos afirmar que:
Juntando todas essas informações, o ponto do centro de massa vale:
Prontinho 😊
A primeira parte já foi!
Passo 2
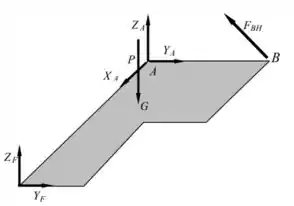
b) Nesse item devemos desenhar o diagrama de corpo livre DCL da placa e da barra.
O bizu pra DCL é sempre começar identificando as forças que agem no corpo.
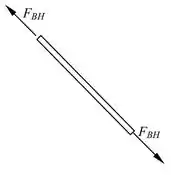
Na barra , como ela está articulada nos dois nós, e , é como as barras de treliça, lembra? Atua uma força axial. Assim:
Agora para a placa, temos as reações em cada um dos apoios. Em , temos um apoio do 3° gênero, logo há reações nos eixos. Em , temos um apoio do gênero, com reações em dois eixos e .
Por fim, em vamos ter a reação da força , puxando a placa na direção axial da barra .
Não podemos esquecer também da força peso, agindo em , tá galera?
Passo 3
c) Devemos calcular as reações no anel em e na articulação em .
Pra fazer isso, não tem muito pra onde correr, sabemos que o sistema está em equilíbrio estático. Esse fato, nos dá duas equações:
Bora começar calculando a resultante de forças da placa.
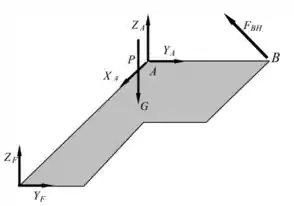
Logo:
Top! Como essa é uma equação vetorial, dela podemos tirar equações escalares:
Agora, vamos calcular o momento em relação ao ponto (é uma boa escolher esse ponto pois é onde temos o maior número de forças sendo aplicadas).
Lembrando que:
Substituindo na equação do momento, temos:
Massa! Temos novamente uma equação vetorial, dela podemos tirar equações escalares:
Bouaaa! Temos equações e variáveis .
Passo 4
Agora é só resolver o sisteminha que encontramos:

De , vem:
De , temos:
De , temos:
De , temos:
Por último, de , temos:
Prontinho! Matamos o sistema 😊
Logo, a reação na articulação em vale:
Já a reação no anel, vale:
Aeee, finalmente né hahaha
Passo 5
d) Pra encerrar devemos determinar o valor de .
Mas, pelo próprio sistema que resolvemos anteriormente, temos:
(tração)
E é isso galera, espero que vocês tenham entendido bem!
Vamo aproveitar o embalo e já ir pra próxima 😊
Resposta
a)
b) Resolução no texto.
c)
d)
(tração)