Determine as coordenadas do centróide da área sombreada.
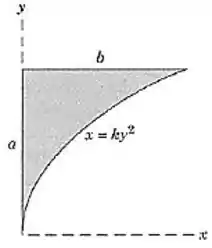
Passo 1
Legal, o nosso primeiro passo é descobrir quem é
Para isso, perceba que para temos , então vamos pegar a equação da curva e substituir isso nela:
Assim, a equação da curva pode ser escrita assim:
Passo 2
Agora vamos calcular a área da região sombreada, vamos calcular a área a partir de retângulos horizontais infinitesimais, que tem a base igual a e altura igual a , como mostrado:
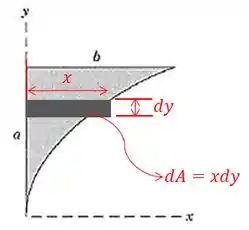
Observe que a área de cada retângulo é dada por:
Dessa forma vamos ter a área da figura como a integral desses retângulos:
Sabendo que é:
Vamos substituir isso dentro da nossa integral e resolver sabendo que varia de zero até :
Agora que temos a área vamos achar os centroides, lembrando que temos de achar o centroide para ambos os eixos e isso pode ser feito através das seguintes equações:
Passo 3
Agora vamos achar o Para isso, usamos:
O dentro desta integral indica a distância horizontal de cada retângulo infinitesimal que criamos até o nosso eixo, assim:
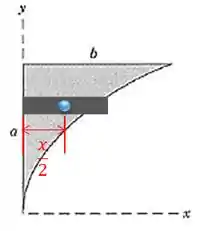
Isso porque sabemos que o centróide de um retângulo fica na metade do seu comprimento. Então, vamos ter que:
E ficamos então com:
Vamos resolver só a parte de cima da equação, para não ficar confuso:
Lembrando que , então:
Pronto, achamos a parte de cima da nossa equação:
Passo 4
Agora vamos calcular :
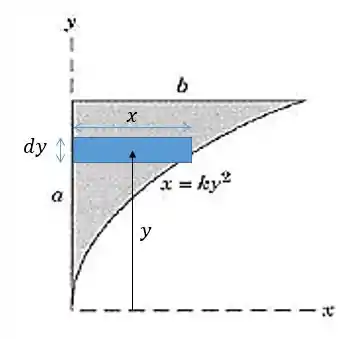
O é a distância vertical de cada retângulo infinitesimal até o eixo horizontal.
Sabendo que e , temos que:
Vamos novamente resolver só a parte de cima da equação e sabendo que varia de zero até , temos:
Pronto, agora podemos achar sabendo que já calculamos a área desta figura no :