Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centros e Centróides

Ver Teoria
Exercício 61234578910111213

Enunciado

Determine a coordenada y do centróide da área sob a curva senoidal mostrada.

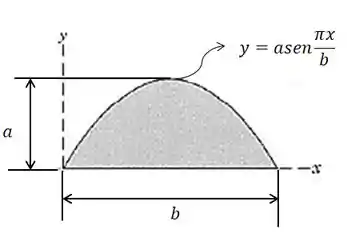
Dica: ∫ s e n 2 x = - 1 4 s e n 2 x + x 2 + c  

Passo 1

Vamos usar aqui novamente a nossa relação:

y - = ∫ y d A A

∴

y - . A = ∫ y d A

Passo 2

Nós podemos começar calculando a área A :

A = ∫ d A

Mas quem é d A ? d A vale:

d A = y d x

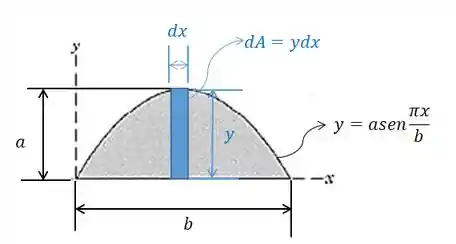
Mas sabemos a equação da curva:

y = a s e n π x b

Substituindo isso na equação de d A , temos que:

d A = y d x         →           d A = a s e n π x b d x

Então, sabendo que x varia de zero até b , a área fica:

A = ∫ d A         →           A = ∫ 0 b a s e n π x b d x

∴

A = - a b π cos ⁡ π x b | 0 b

Aplicando os limites 0   até   b :

A = - a b π cos ⁡ π b b + a b π cos ⁡ 0

∴

A = 2 a b π

Passo 3

Agora vamos calcular a parte de cima da equação de y - :

∫ y d A

Perceba que y , nesse caso, se refere à distância vertical do centroide de cada retângulo que criamos até o eixo horizontal.

Então:

y = y 2 = a 2 s e n π x b

Lembrando que d A = a s e n π x b d x , então podemos escrever:

∫ y d A = ∫ a 2 s e n π x b a s e n π x b d x

O intervalo de integração de y vai de zero até b , então:

∫ y d A = ∫ 0 b a 2 2 s e n 2 π x b d x

Aplicando a dica que foi dada no enunciado da questão:

∫ 0 b a 2 2 s e n 2 π x b d x = a 2 2 ∫ 0 b s e n 2 π x b d x = a 2 2 - b 4 π s e n 2 π x b + x 2 0 b

Aqui eu usei a fórmula:

s e n 2 π x b = 1 - cos ⁡ 2 π x b 2

Assim:

∫ 0 b a 2 2 s e n 2 π x b d x = a 2 2 - b 4 π s e n 2 π + b 4 π s e n 0 + b 2 - 0 2

∴

a 2 2 b 2 = a 2 b 4

Passo 4

Por fim, só aplicar:

y - = ∫ y d A A           →             y - = a 2 b 4 2 a b π

∴

y - = π a 8

Resposta

y - = π a 8

Exercícios de Livros Relacionados

Calcule o centroide da área abaixo em termos das variáveis dos raios:
A barra esbelta homogênea tem uma seção transversal uniforme e está dobrada na forma mostrada. Calcule a coordenada y do centro de massa da barra. (Lembrete: O comprimento do arco diferencial é d L =
Determine a coordenada z do centroide do volume obtido pela revolução da área triangular sombreada de 360° em torno do eixo z.
Localize o centro de massa do corpo sólido homogêneo cujo volume é determinado pela revolução da área sombreada de 360° em torno do eixo z.
Specify the x-, y-, and z-coordinates of the mass center of the homogeneous semicylinder.