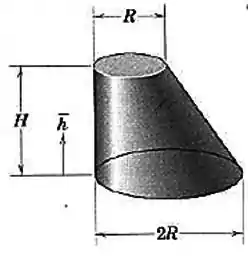
O corpo afilado tem uma seção transversal horizontal circular. Determine a altura de seu centro de massa, acima da base do sólido homogêneo.
Passo 1
Neste exercício queremos achar o centro de massa, então vamos usar essa fórmula aqui:
Para isso, temos que definir o que será o nosso . Mas para isso você precisa lembrar que o cálculo da massa de um corpo que tem uma massa específica é:
Onde é o volume do corpo. Se derivarmos ambos os lados dessa equação, vamos ter que:
Então, o que precisamos definir na nossa figura é um elemento de volume . Para isso, vamos criar cilindros de espessura infinitesimal. Vendo de frente nossa figura fica assim:
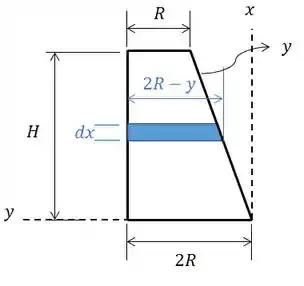
Repare que é a equação da reta que limita o lado direito da nossa figura.
Mas estamos criando cilindros de espessura bem pequena, assim:
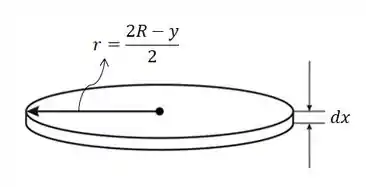
Então, o volume deste cilindro fica assim:
Onde é a altura e é o raio. Mas como temos uma espessura bem pequena, nosso volume será bem pequeno também:
Agora vamos substituir na nossa equação de :
Elevando o termo de dentro dos parênteses ao quadrado, temos:
Passo 2
Nosso próximo passo é achar a equação da reta que limita o lado direito da nossa figura. Para isso, sabemos que uma equação da reta genérica tem o seguinte formato:
E quando temos que , então a nossa equação fica:
E quando temos que e agora a nossa equação fica:
Então, a equação da reta fica:
Passo 3
Agora vamos substituir a equação da reta que acabamos de achar na nossa equação de :
Vamos colocar para fora dos parênteses:
Passo 4
Agora vamos achar a massa do nosso corpo e para isso temos que resolver a integral:
Como é constante vamos passá-lo para fora da integral. E sabemos que varia de até , então:
Vamos dividir isso e três integrais para facilitar:
Resolvendo estas integrais, temos que:
Passo 5
Agora vamos achar o termo de cima na nossa equação:
Repare que o de dentro da integral é a distância do centroide do cilindro que criamos até o eixo horizontal:
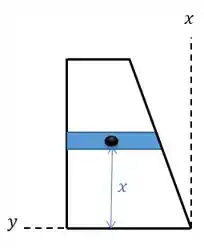
Ou seja, vamos calcular :
Vamos passar o termo que é constante para fora da integral:
Vamos separar em três integrais sabendo que varia de até :
Passo 6
Pronto, agora é só substituirmos na fórmula para achar a coordenada de :
Então, a altura do centro de massa do sólido é: