Determine as coordenadas e do centróide da área sombreada.
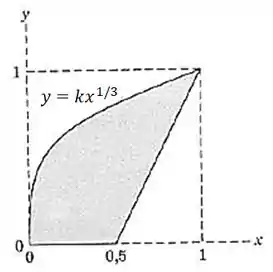
Passo 1
Estamos procurando as coordenadas eda área da figura. Uma das equações nós sabemos:
Quanto vale ? Sabemos que quando o valor de também é , então vamos substituir isso na nossa equação:
Dessa maneira, ficamos com esta equação aqui:
Mas e a equação da reta? Vamos ter que descobrir... Sabemos que uma equação da reta genérica tem a seguinte equação:
E que quando temos que , então vamos substituir isso na nossa equação genérica:
E perceba também que quando temos que , vamos substituir isso novamente na nossa equação genérica:
Agora temos um sistema:
Como sabemos que , vamos substituir isso na primeira equação do sistema:
E vai valer:
Então, a equação da reta fica:
Passo 2
Para achar o , vamos usar as equações em função de já que assim vai ficar mais fácil:
E:
Vamos criar retângulos para fazer a integração de modo que será:
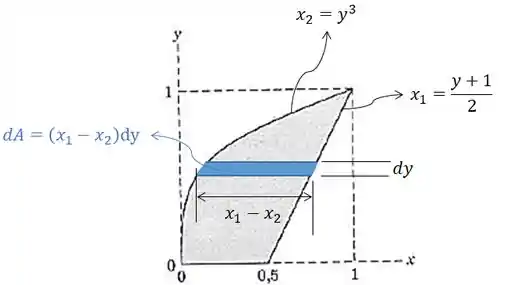
Passo 3
Vamos começar calculando a área da região sombreada. A área que está entre as duas curvas acima vai ser dada por:
Sabendo que varia de até , vamos ter que:
Podemos dividir isso em três integrais para facilitar a resolução:
Passo 4
Agora vamos resolver o termo de cima na nossa equação de :
O dentro da integral é a distância do centróide de cada retângulo até o eixo horizontal:
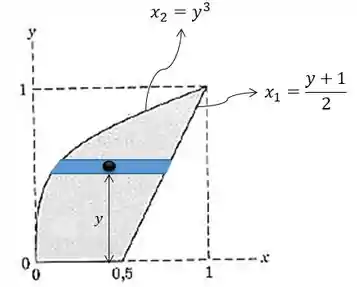
Sabendo que:
Então, será:
Separando em três integrais, vamos ter que:
Então, a nossa coordenada será:
Passo 5
Vamos calcular agora a coordenada . Para isso, vamos calcular o termo de cima da fórmula:
O dentro da integral é a distância do centróide do retângulo que criamos para integrar até o eixo vertical. Essa distância é a média entre as duas funções, assim:
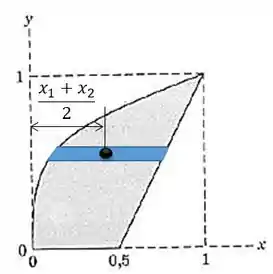
Vamos ter que será:
Sabendo que continua o mesmo:
Então:
Repare que usamos a propriedade que diz que:
Substituindo as funções de e , temos que:
Agora sim podemos calcular a coordenada :