Calcule a distância medida desde a base até o centróide do volume do cone truncado.
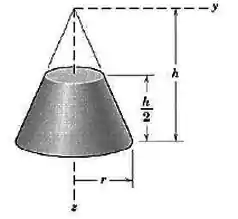
Passo 1
Vamos desenhar um esquema do cone:
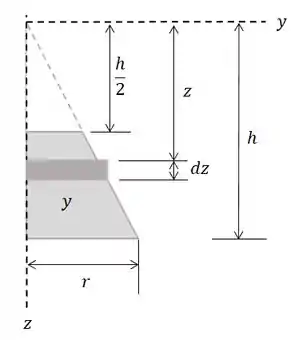
Repare que a orientação de aponta para baixo.
Depois voltaremos para ele. Vamos agora calcular o volume.
Para isso vamos criar um círculo de raio e espessura infinitesimal :
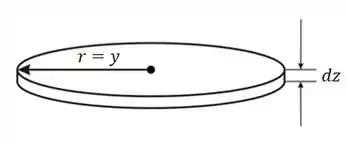
Agora, para se calcular , temos que escrever uma função em função de .
Passo 2
Note que o contorno do cone é uma reta. Vamos girar a figura para facilitar a visualização:
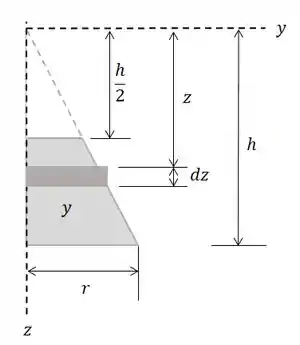
Perceba que cresce conforme cresce, sendo o , e o
Assim, sendo:
Para , temos que
E quando , temos que
Assim:
Passo 3
Show de bola. Agora podemos calcular o volume, sabendo que e que:
Obs: Perceba que o limite inferior é pois se trata de um tronco de cone que começa em e termina em .
Resolvendo esta integral, temos que:
Aplicando os limites:
Passo 4
Para calcular , temos que aplicar:
Temos que calcular , sabendo que e que, então:
Passo 5
Assim:
E como ele tá pedindo a altura da base até o centroide: