Localize o centróide da área sombreada entre as duas curvas.
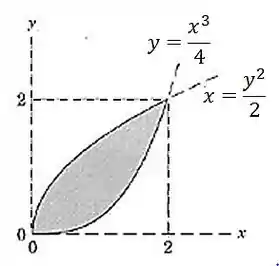
Passo 1
Em primeiro lugar, vamos escrever ambas as equações em função de . A primeira já está:
E a segunda equação fica assim:
Show de bola?
Passo 2
Agora vamos calcular a área da figura:
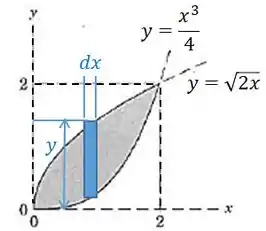
Perceba que a área vai ser o somatório tendendo ao infinito, ou seja, uma integral, dos pequenos retângulos. A área de cada retângulo, por sua vez, é dada por:
Mas o limite superior do retângulo é dado pela equação e o limite inferior pela equação , então podemos escrever que é a diferença entre as funções:
Como varia de zero até , podemos dizer que a área é:
Assim:
Agora podemos usar as duas relações abaixo:
Passo 3
Vamos então calcular primeiro .
O dessa equação, no caso, é o próprio já que a distância de cada retângulo infinitesimal até a origem é justamente
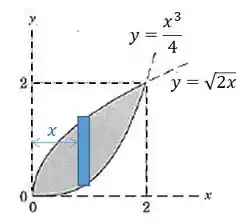
Lembrando que , então:
Resolvendo isso, temos que:
Passo 4
Agora vamos calcular :
Como estamos lidando agora com a componente vertical, cada vai ser a média das funções:
Assim:
E sabemos que , então:
Lembra disso aqui:
Vamos usar isso para os termos dentro da integral:
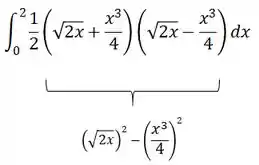
Ficamos com isso aqui:
Passo 5
Pronto! Agora é só aplicar:
E: