Sejam os vetores e em
Escreva o vetor como combinação linear de e
Para que valor de o vetor é combinação linear de e ?
Determinar uma condição entre e para que o vetor seja uma combinação linear de e .
Passo 1
Letra
Para escrever o vetor como de queremos o seguinte:
Ou seja, temos que achar os coeficientes de que satisfazem essa equação:
Podemos montar um sistema com os coeficientes
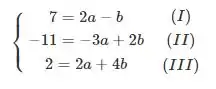
Vamos isolar na :
Agora substituímos em :
E por fim substituímos o valor de para encontrar
Passo 2
Muita calma agora! Se o sistema só tivesse as equações e estaria sussa e poderíamos terminar por aqui. Entretanto, jovem padawan, temos que ver se os resultados achados satisfazem a outra equação não usada, no caso a :
Ufa! Deu tudo certo! Então a nossa combinação fica assim:
Não se esqueça de sempre conferir isso ;)
Passo 3
Letra
Mesma coisa que a letra
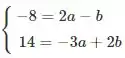
Na primeira equação podemos isolar o :
E substituir na segunda equação:
E por fim podemos encontrar o valor de :
Bom, percebe que temos equações? Então, com as duas primeiras já dá pra achar . Mas e a terceira serve pra que??? Bom a gente pega os valores de e substitui para achar :D:
Encontrando :
Passo 4
Letra
Para determinar um condição precisamos montar uma com o vetor . Desta vez vou chamar os coeficientes de de respectivamente.
Vamos montar o sistema:
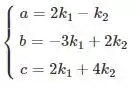
Vamos primeiro isolar o na primeira equação:
E substituir na segunda equação para encontrar em função de :
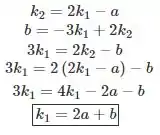
Podemos voltar na primeira equação e encontrar o valor desubstituindo o valor de :
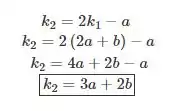
E por fim , substituir os valores de e na terceira equação para encontrar o valor de em função de :
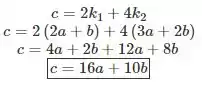
Em outras palavras, o que resolvi aí em cima, foi achar os coeficientes que satisfaçam a combinação linear que estipulamos. Como consequência desses resultados, conseguimos achar uma relação entre necessária para existir a combinação linear.
Resposta