Elétrons podem exibir um comportamento ondulatório. Numa experiência de difração, elétrons não relativísticos com energia cinética incidem sobre uma fenda de largura . Um detetor sobre uma tela a uma distância pode ser deslocado ao longo da direção , conforme a figura.
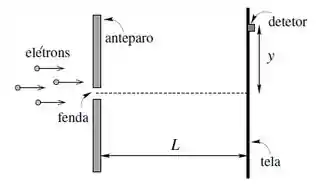
- Expresse o comprimento de onda de de Broglie dos elétrons em termos da sua energia cinética .
- Qual é o menor valor para a posição do detetor onde não são observados elétrons?
Passo 1
Letra a)
A energia cinética de uma partícula se relaciona com seu momento linear.
Assim, o comprimento de onda de de Broglie fica:
Passo 2
Letra b)
Podemos considerar esse como sendo um experimento de difração por fenda simples, onde a onda incidente (os elétrons) têm o comprimento de onda calculado na letra .
Nós nunca encontraremos elétrons onde seriam “franjas escuras”, que correspondem com mínimos de difração.
A condição para achar o mínimo de difração é (Essa condição só vale para ):
Para ângulos bem pequenos, podemos fazer:
Sendo que a tangente é dada pela geometria do problema:
O primeiro mínimo corresponde a , e teremos então:
Resposta
Letra
Letra