Um estudante de laboratório de Física Moderna realiza um experimento para estimar a constante de Planck e a função trabalho de um material, observando o efeito fotoelétrico.
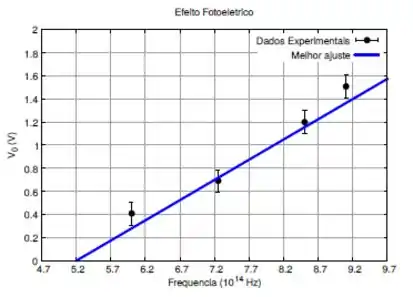
Os pontos experimentais obtidos do potencial de freamento versus a frequência da luz incidente estão no gráfico a seguir. A curva contínua representa a reta que melhor se ajusta aos dados experimentais.
Baseando-se apenas no gráfico, a função trabalho do material é estimada pelo valor:
Passo 1
O “potencial de freamento” (ou potencial de corte) de um material se relaciona com a frequência através da seguinte equação:
Assim, temos que encontrar a equação da reta de melhor ajuste dos pontos experimentais e encontrar o coeficiente angular e linear.
Onde teremos:
Passo 2
Para encontrar e , usamos dois pontos quaisquer da reta. Do gráfico, quando .
O outro ponto que podemos observar melhor é quando , tendo .
Substituindo a igualdade anterior:
O que dá para :
Ao multiplicarmos esse valor pela carga do elétron, podemos achar a energia em unidade de elétrons volt, dando:
A resposta então é a letra d).
Resposta
Letra (d)