Em um experimento do efeito fotoelétrico foi encontrado o potencial de corte em função dos comprimentos de onda no lítio, como representado na figura
A partir da informação contida na figura, determine:
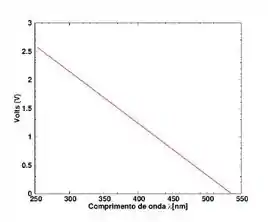
a) O valor da constante de Planck
b) A função de trabalho do lítio (em eV)
Passo 1
Para resolvermos essa questão vale lembrar alguns detalhes importantes.
A primeira coisa a se notar é que a nossa função é um reta, logo, a sua equação tem que seguir a equação y=Ax+B, até aqui tudo bem, mas o que é mais importante ainda notar?
A fórmula geral do efeito foto elétrico é dada por
Em que é a carga que nesse efeito é a carga do elétron, é o que chamamos de diferença de potencial ou ainda potencial de corte, é a frequência do fóton e que é a energia de ligação dos elétrons a superfície que chamamos de função trabalho do Material.
Se dividirmos toda a função por teremos que
Em que essa função representa uma reta onde
Sabendo isso , podemos determinar facilmente o valor de h pelo coeficiente angular da nossa reta, tomando alguns cuidados muito importante
Passo 2
Sabemos que podemos escrever o nosso coeficiente angular da seguinte maneira
Em que
Logo teremos
Mas vale lembrar que a frequência do fóton é calculada por
Substituindo teremos
Isolando h teremos
Agora basta pegar os valores na tabela. Pegando os valores finais e iniciais teremos
Substituindo esses valores na função teremos
Passo 3
Para acharmos a função trabalho do lítio basta substituir um dos valores encontrados na equação do efeito fotoelétrico
Substituindo os valores e isolando a função trabalho do lítio encontraremos que
Resposta
a)
b)