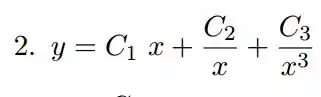Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Euler de Ordem Superior

Ver Teoria
Exercício 41235678910111213

Enunciado

Passo 1

Essa é uma equação do tipo Cauchy-Euler. Nessas EDOs, resolvemos utilizando a substituição

y x = x r

Para isso precisamos encontrar as derivadas

y ' x = r x r - 1

y ' ' x = r r - 1 x r - 2

y ' ' ' x = r r - 1 r - 2 x r - 3

Passo 2

Substituindo na equação ficamos com

x 3 r r - 1 r - 2 x r - 3 + 6 x 2 r r - 1 x r - 2 + 3 x r x r - 1 - 3 x r = 0

r r - 1 r - 2 x r + 6 r r - 1 x r + 3 r x r - 3 x r = 0

Colocando x r em evidência

r r - 1 r - 2 + 6 r r - 1 + 3 r - 3 = 0

Agora precisamos encontrar as raízes dessa equação

r r 2 - 2 r - r + 2 + 6 r 2 - 6 r + 3 r - 3 = 0

r 3 - 3 r 2 + 2 r + 6 r 2 - 3 r - 3 = 0

r 3 + 3 r 2 - r - 3 = 0

r 2 - 1 r + 3 = 0

Logo as raízes são

r 1 = 1 ; r 2 = - 1   e   r 3 = - 3

Passo 3

Agora só falta substituir as raízes na nossa solução geral

y x = C 1 x r 1 + C 2 x r 2 + C 3 x r 3

Ficamos com

y x = C 1 x + C 2 x + C 3 x 3

Fim!

Resposta

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 6, determine os intervalos nos quais existem, com certeza, soluções.6. ( x 2 - 4 ) y 6 + x 2 y ' ' ' + 9 y = 0
Em cada um dos problemas de 7 a 10, determine se as funções dadas são linearmente dependentes ou linearmente independentes. Se forem linearmente dependentes, encontre uma relação linear entre elas.7.
Em cada um dos problemas de 1 a 6, determine os intervalos nos quais existem, com certeza, soluções.1. y ( 4 ) + 4 y ' ' ' + 3 y = t
Em cada um dos problemas de 1 a 6, determine os intervalos nos quais existem, com certeza, soluções.2. t y ' ' ' + ( s e n t ) y ' ' + 3 y = c o s t
Em cada um dos Problemas 41 e 42, mostre que o ponto x = 0 é um ponto singular regular. Tente, em cada problema, encontrar soluções da forma ∑ n = 0 ∞ a n x n . Mostre que (exceto por múltiplos consta