Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equações Adimensionalizadas

Ver Teoria
Exercício 51234678910111213

Enunciado

Adimensionalize a equação da energia e sua condição de contorno definindo T * =   T / T 0 , em que T 0 é a temperatura de entrada, considerada constante. Use outras variáveis adimensionais, se necessário conforme indicado abaixo. Isole todos os parâmetros adimensionais que você encontrar e verifique se já são conhecidos.

Equação da Energia

ρ c p d T d t = k ∇ 2 T + Φ

Onde k é coeficiente de condutividade térmica e Φ é a função de dissipação viscosa

Condição de contorno

T f l u i d o = T p a r e d e

Variáveis adimensionais

x * = x L         y * = y L       z * = z L  

t * = t U L

Passo 1

Essa equação pode parecer um pouco complicada por causa das derivadas de temperatura...

ρ c p d T d t = k ∇ 2 T + Φ

Aliás, não vamos nos esquecer que essa equação pode ser aberta assim:

ρ c p d T d t = k ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 + ∂ 2 T ∂ z 2 + Φ

Maaas, o enunciado foi maneiro com a gente e já deu as variáveis adimensionais para a gente começar! Isso vai nos poupar muitas contas. Então vamos lá?

Essas são as variáveis da equação original

ρ , c p , T , t , k ,   x , y , z , Φ

São nove variáveis. Suas dimensões são:

ρ = M L - 3

T =   Θ

c p = M L T - 2 L M Θ =   L 2 T - 2 Θ - 1

t = T

k =   M L T - 2 L T - 1 L Θ = M L T - 3 Θ - 1

x = L

y = L

z = L

Φ =   M L - 1 T - 3  

Temos então 4 dimensões. Logo, 9 - 4   =   5 grupos pi

O enunciado já dá 5 variáveis adimensionais! Olha aí

x * = x L   ⇒ x = L x *

y * = y L ⇒ y = L y *

  z * = z L ⇒ z = L z *

t * = t U L ⇒ t = L U t *

T * =   T / T 0 ⇒ T = T 0 T *

Então, já vamos substituir na equação original no próximo passo. Nos poupou o trabalho de calcular cada grupo pi 😉

Passo 2

Equação original:

ρ c p d T d t = k ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 + ∂ 2 T ∂ z 2 + Φ

Substituindo as variáveis adimensionais

ρ c p d T 0 T * d L t * U = k ∂ 2 T 0 T * ∂ L x * 2 + ∂ 2 T 0 T * ∂ L y * 2 + ∂ 2 T 0 T * ∂ L z * 2 + Φ

ρ c p U T 0 L d T * d t * = k T 0 L ∂ 2 T * ∂ x * 2 + ∂ 2 T * ∂ y * 2 + ∂ 2 T * ∂ z * 2 + Φ

Isolando d T * / d t *

d T * d t * = k T 0 L L ρ c p U T 0 ∂ 2 T * ∂ x * 2 + ∂ 2 T * ∂ y * 2 + ∂ 2 T * ∂ z * 2 + L ρ c p U T 0 Φ

d T * d t * = k ρ c p U ∂ 2 T * ∂ x * 2 + ∂ 2 T * ∂ y * 2 + ∂ 2 T * ∂ z * 2 + L ρ c p U T 0 Φ

Podemos escrever assim também:

d T * d t * = k ρ c p U ∇ 2 T * + L ρ c p U T 0 Φ

Quase toda a equação está adimensionalizada, mas Φ ainda não está escrita da forma adimensional. Lembrando que

Φ =   M L - 1 T - 3

Φ =   M L - 1 T - 1 T - 2

Sendo que M L - 1 T - 1 é a dimensão da viscosidade. Para garantir o T - 2 , podemos multiplicar pela razão entre velocidade e comprimento de referência ao quadrado. Hã? Calma que eu te mostro na equação:

Φ =   μ U 2 L 2 Φ *

Conferindo as dimensões:

μ U 2 L 2 =   M L - 1 T - 1 ( L T - 1 ) 2 L 2 = M L - 1 T - 1 L 2 T - 2 L 2

μ U 2 L 2 =   M L - 1 T - 1 T - 2 = M L - 1 T - 3

Que é a mesma unidade de Φ , o que deixa ele adimensional, como queria te mostrar 😉

Voltando à equação

d T * d t * = k ρ c p U ∇ 2 T * + L ρ c p U T 0 Φ

Substituindo Φ =   μ U 2 L 2 Φ *

d T * d t * = k ρ c p U ∇ 2 T * + L ρ c p U T 0   μ U 2 L 2 Φ *

Organizando

d T * d t * = k ρ c p U ∇ 2 T * + U 2 c p T 0   μ   ρ U L Φ *

Estamos chegando lá! Essa é a equação adimensionalizada. Mas, será que esses números adimensionais aí são conhecidos?

Passo 3

Primeiro, vamos pensar no nosso amigo Reynolds. Onde ele está?

R e =     ρ V D μ o u   R e =   ρ U L μ

Logo:

d T * d t * = k ρ c p U ∇ 2 T * + U 2 c p T 0   1   R e Φ *

Show! Faltam 2 números adimensionais. Esses não são tão conhecidos. Geralmente, uma tabela é fornecida para você encontrá-los. Uma tabela parecida com essa, por exemplo:

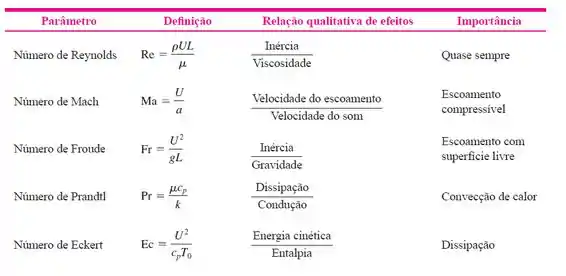
E aí, a gente vê que o número de Eckert está na nossa equação também

d T * d t * = k ρ c p U ∇ 2 T * + E c   1   R e Φ *

Além disso, ρ c p U / k é conhecido como Número de Péclet. Logo:

d T * d t * = 1 P e ∇ 2 T * +   E c R e Φ *

Passo 4

Finalmente, para adimensionalizar a condição de contorno, vamos nos basear nas referências que já foram assumidas.

T f l u i d o = T p a r e d e

A temperatura de referência é a temperatura de entrada T 0 , logo

T * f l u i d o p a r e d e =   T p a r e d e T 0

YES! Encontramos tudo que o exercício pediu! :D

Resposta

d T * d t * = 1 P e ∇ 2 T * +   E c R e Φ *

T * f l u i d o p a r e d e =   T p a r e d e T 0

Apareceram o número de Reynolds R e , Péclet ( P e ) e Eckert ( E c )

Exercícios de Livros Relacionados

A inclinação da superfície livre de uma onda em regime permanente em um escoamento unidimensional em uma camada de líquido pouco profunda é descrito pela equação ∂ h ∂ x = - u g ∂ u ∂ x Use um escala
A equação que descreve a vibração de pequena amplitude de uma viga é ρ A ∂ 2 y ∂ t 2 + E I ∂ 4 y ∂ x 4 = 0 em que y é a deflexão da viga no local x e no tempo t , ρ e E são a massa específica e o módu
O teorema de transporte de Reynolds (TTR) é discutido no Capítulo 4. Para o caso geral de um volume de controle móvel c/ou deformável, escrevemos o TTR da seguinte maneira:onde V r → é a velocidade re
Uma aplicação importante da mecânica dos fluidos é o estudo da ventilação de uma sala. Em particular, suponhamos que há uma fonte 5 (massa por unidade de tempo) de poluição do ar em uma sala de volume
Considere a ventilação de uma sala bem misturada como aquela da Figura P7-25. A equação diferencial da concentração de massa na sala como função do tempo é dada no Problema 7-25 e é repetida aqui por