Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 4, Seção 1, Questão 57.
(Cap 4 – Ex 57) Uma caixa de está sobre uma rampa sem atrito inclinada de . Alguém puxa a caixa rampa acima com uma corda (Figura 4-44). Se a corda forma um ângulo de com a horizontal, qual é a menor força capaz de deslocar a caixa rampa acima?
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
O diagrama de corpo livre, mostra as forças que estão agindo na caixa quando o homem a puxa sobre a superfície sem atrito. Podemos aplicar a segunda lei de Newton para encontrar a força mínima necessária para mover a caixa.
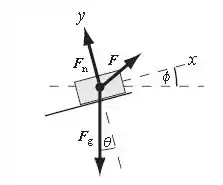
Perceba que foram inseridas linhas tracejadas representando os eixos e . Por que elas são necessárias? As forças são divididas em componentes de força. Mas como assim? No caso das Tensões aplicadas em um ângulo inclinado, por exemplo, não podemos dizer que essa determinada tensão exerce força na vertical OU na horizontal e sim devemos dizer que exerce força na vertical E na horizontal, ou seja, uma parcela da tensão é depositada para o componente e uma parcela no componente . E se a tensão estiver sobre um eixo? Isso significa que a componente desse eixo será igual a própria tensão e a componente no eixo oposto será zero.
Beleza, entendi toda essa teoria, mas onde isso irá me ajudar?
Por definição, temos que:
A somatória de forças (tensões) sobre o eixo é igual ao produto entre a massa e a aceleração gravitacional no eixo . O mesmo vale para o eixo . A somatória das tensões sobre é igual ao produto entre a massa e a aceleração gravitacional no eixo .
Para concluir, para que os sistemas se encontrem em repouso, e devem ser iguais a zero. Caso não fosse zero, então o sistema estaria em movimento.
Portanto:
Substituindo os valores, temos:
Isso é a Física! Doce como o mel...
Para essa questão é isso pessoal! Bora resolver mais uma?
