4. Considere uma vasilha semiesférica de raio (conforme a figura acima à direita). Um cubo de gelo de massa cai da borda da vasilha (desconsidere o atrito).
e) Qual a força que a vasilha exerce sobre o cubo de gelo quando este passa ponto assinalado na figura.

Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉

Nessa questão a situação é a seguinte: temos uma vasilha semiesférica de raio e na borda dessa vasilha cai um cubo de gelo de massa . Com esse problema, queremos obter a força que a vasilha faz no cubo de gelo no ponto dado na figura.
E aí, como fazemos isso? 🤔
Em outras palavras, queremos obter a força normal sofrida pelo cubo no instante em que o cubo passa pelo ponto mais baixo da vasilha.
Preparado? Bora começar! 😉
Passo 2
Primeiramente vamos analisar as forças que agem sobre o cubo no ponto
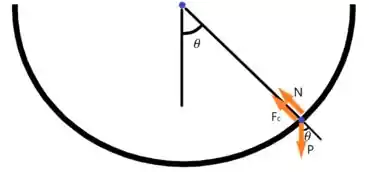
Como não aponta na direção radial, temos que obter a componente que age nesse sentido.
Pela lei dos cossenos, temos que
Como o sistema está em equilíbrio, podemos dizer que o somatório das forças que atuam para cima é igual ao somatório das forças que atuam para baixo, ou seja, a força peso é igual a soma da força normal com a força centrípeta
Sabemos que a força peso é dada por
Já a força centrípeta por
Lembra disso? 👀
Passo 3
Substituindo na equação do problema, temos
Anteriormente, vimos que a velocidade do cubo de gelo nesse instante é dada por
Substituindo em
Sacou como faz? Responde Aí! 😉
