Um cilindro com peso está em equilíbrio sobre um piso horizontal e encostado em uma parede vertical, como indica a figura abaixo. Uma força de módulo constante, vertical, para cima, é aplicada na lateral esquerda do cilindro. O valor de é o maior possível para este equilíbrio. Os coeficientes de atrito estático do cilindro com o piso e com a parede são iguais a. Seja o modulo da forca normal do piso sobre o cilindro e o módulo da força normal da parede sobre o cilindro. Determine, sem arredondar, a parte inteira das razões:
- .
(Lembrete: )
Passo 1
O primeiro passo a se fazer para que possamos calcular as razões é fazer o diagrama de forças que atuam sobre o cilindro:
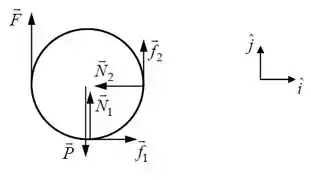
Aqui temos dois atritos: um com o chão e outro com a parede vertical. Temos também duas normais, uma com a parede e outra com o chão!
Com o diagrama definido, podemos escrever o equilíbrio de rotação e de translação para o cilindro.
Equilíbrio de translação:
(1)
(2)
Equilíbrio de rotação (eixo z = eixo do cilindro, saindo do papel; R = raio do cilindro):
(3)
Lembrando que as normais e o peso não exercem torque por que apontam na direção do centro de rotação (que nesse caso é o centro do cilindro mesmo!)
Passo 2
A condição de máximo de implica no valor máximo para o atrito estático. Da equação (1), segue que:
Como
Logo a razão é:
Passo 3
Da equação (3) temos que
No passo anterior vimos que . Já é , assim
No passo anterior também chegamos a , ou seja
Calculando a razão
Resposta
a) 5
b)