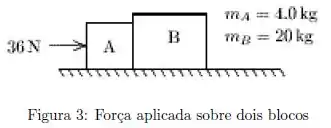
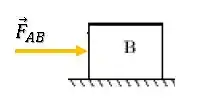
Dois blocos (A e B) estão em contacto sobre uma superfície horizontal sem atrito. Uma força constante de é aplicada ao bloco A, como mostrado na figura 3. O módulo da forca que A exerce sobre B é:
(a)
(b)
(c)
(d)
(e)
Passo 1
O bloco A é empurrado por uma força de e consequentemente empurra o bloco B com uma força de contato que chamaremos de .
Se não há atrito, a única força na direção da aceleração do bloco B é a força que A exerce sobre B:
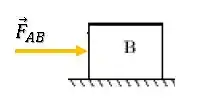
Então, podemos encontrar essa força a partir da segunda lei de Newton:
Temos a massa , porém não sabemos a aceleração do bloco B.
Passo 2
Você concorda que como um bloco está sempre em contato com o outro, eles se moverão com a mesma aceleração?
Sim, né!
Então, temos que a aceleração do bloco A é a mesma aceleração do bloco B e portanto a mesma aceleração do sistema (os dois blocos).
Então, podemos descobrir essa aceleração analisando o sistema (os dois blocos em conjunto).
Temos que lembrar que aquela força que A exerce em B terá uma força de reação que B exerce em A . Essas forças internas sempre se anulam:
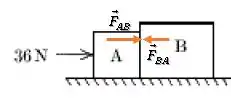
Sobre as forças externas, temos as forças peso e normal na vertical, mas elas se anulam já que a aceleração está na horizontal.
A força externa resultante será a própria força de :
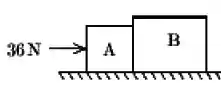
Então, aplicando a segunda lei de Newton para o conjunto, temos:
Com isso, a aceleração do bloco B também será:
Passo 3
Agora que temos a aceleração de B, podemos aplicar a segunda lei de Newton para ele:
Ficamos com a letra (d).
Resposta
Letra (d)