Um corpo de massa , inicialmente em repouso no instante inicial , é submetido a uma força dependente do tempo , onde é uma constante positiva e é um vetor unitário que faz um ângulo fixo com o eixo horizontal, conforme mostrado na figura abaixo. O coeficiente de atrito estático entre o corpo e a superfície é enquanto o coeficiente de atrito dinâmico (cinético) é .
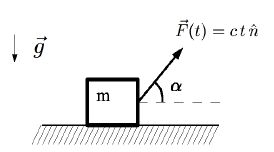
(a) Faça um diagrama das forças que atuam no corpo no instante inicial e escreva tais forças num sistema de coordenadas apropriado.
(b) Encontre quanto tempo leva para a corpo começar a se movimentar e também o tempo que leva para o corpo “perder” contato com o solo.
(c) Encontre o vetor posição e o vetor velocidade do corpo no instante em que o mesmo perde contato com o solo. Deixe sua resposta em termos de e e demais quantidades fornecidas no enunciado.
Passo 1
O que tem de “diferentão” nessa questão é essa força variando com o tempo:
Esse vetor unitário apenas diz a direção para a qual aponta a força, mas como o próprio nome já diz, ele tem módulo igual a , então ele não altera em nada o módulo de .
Além disso, a expressão de mostra que essa força começa nula:
Mas conforme o tempo vai aumentando, a força vai aumentando também e de forma linear “”.
Beleza, vamos aos itens.
Passo 2
Na letra (a), queremos o diagrama de forças no instante inicial.
Como vimos no Passo 1, temos que a força inicialmente é nula:
Então, restam apenas as forças peso para baixo e a normal para cima:
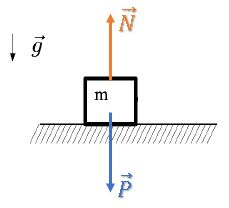
Além disso, ele pede para a gente deixar claro um sistema de referências.
Vamos adotar o sistema de referências padrão na horizontal e na vertical, podemos representar essas direções com as componentes e :
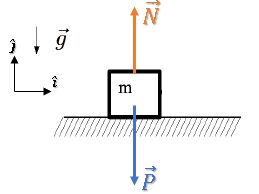
Respondido o item (a).
Passo 3
Na letra (b), queremos duas coisas distintas. Uma delas é o tempo para o corpo começar a se movimentar e a outra é o tempo para o corpo perder “contato” com o solo.
Vamos uma por uma...
Por que ele pede o tempo para o corpo começar a andar se desde o início a força começa a atuar?
O que acontece é que existe uma força de atrito agindo contra a tendência de deslizar do bloco, ou seja, inicialmente a força de atrito estático vai manter esse corpo parado.
Isso vai acontecer até que essa força de atrito atinja seu limite máximo, dado por:
Nesse instante, o corpo ultrapassa o limite máximo da força de atrito e entra em movimento.
Queremos justamente esse tempo.
OBS: Esse limite de força de atrito máxima não é fixo. A força varia no tempo, fazendo a força normal variar e por consequência também varia.
Passo 4
Vamos começar decompondo a força em suas componentes horizontal e vertical, além de considerar uma força de atrito contrária à força :
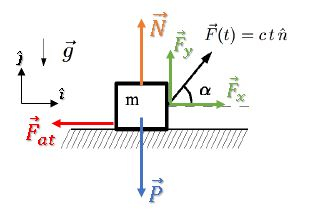
Podemos escrever as componentes de usando o ângulo :
Passo 5
Vamos aplicar a Segunda Lei de Newton:
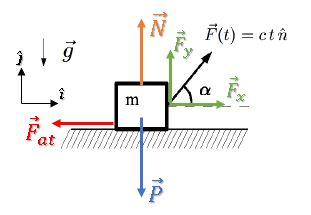
Na horizontal, temos um equilíbrio de forças, já que o corpo começa parado devido ao atrito:
Na vertical, também temos um equilíbrio inicialmente:
Mas o que fazemos com essas equações?
Passo 6
Primeiro queremos o tempo para que o corpo entre em movimento, ou seja, vamos usar a informação de que a força de atrito atingiu seu valor máximo:
Sendo que já achamos uma relação para essa força normal :
Substituindo isso, temos:
Agora, vamos susbtituir esse valor de na equação de equilibrio na horizontal:
Isolando o tempo , e chamando-o de , temos:
Esse é o tempo que o corpo leva para entrar em movimento.
Passo 7
Beleza, vimos que a partir daí o corpo entra em movimento.
Agora, queremos saber quanto tempo ele leva para “perder” o contato com o chão.
Mas por que ele perderia o contato?
Bom, a força tem uma componente atuando perpendicularmente para cima e ela vai aumentando com o tempo até um dado momento em que ela vence a força peso do corpo e consegue suspendê-lo.
Antes disso acontecer, a força que equilibra essa diferença é a força normal , portanto no instante limite, essa força normal será zero, mostrando que o corpo está prestes a perder contato:
Queremos achar esse novo tempo .
Passo 8
Por mais que agora o corpo apresenta uma aceleração na horizontal, a equação de equilíbrio da vertical até o instante limite é a mesma de antes. Então:
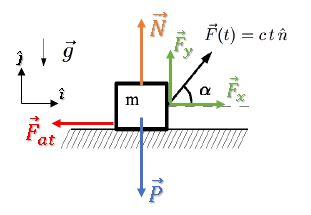
Na vertical:
Mas agora, vamos considerar que em a força normal chega a zero:
Pronto, achamos o instante em que o corpo perde o contato.
Passo 9
Na letra (c), queremos o vetor posição e o vetor velocidade no instante em que o corpo perde o contato .
Para isso, vamos refazer as equações de força resultante, considerando agora que o corpo estava realizando um movimento na horizontal e chega no instante limite de perder o contato.
Como esse é o primeiro instante em que o corpo vai começar a ter um movimento na vertical, é de se esperar que tanto o vetor posição quanto o vetor velocidade ainda estejam na horizontal.
Passo 10
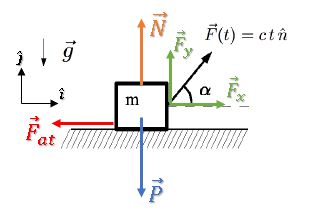
Na horizontal, temos uma aceleração, logo:
A força de atrito cinético é dada por:
Substituindo na primeira expressão, temos:
Já na vertical, temos ainda um equilíbrio de forças (instante antes de perder o contato):
Podemos escrever a força normal em função das outras variáveis para substituir esse valor na equação da horizontal:
Substituindo na equação da horizontal:
Assim, conseguimos uma expressão para a aceleração do corpo:
Como ela varia conforme o tempo , podemos escrever:
Passo 11
Agora segura na minha mão que as expressões não ficam muito bonitas daqui pra frente, mas vai dar tudo certo, relaxa.

Vamos lá, a aceleração é a variação da velocidade, então a aceleração é a derivada da velocidade:
Mas estamos na situação contrária, nós temos a aceleração e queremos achar a velocidade . Então, a gente usa a ferramenta contrária da derivada... a integral.
São apenas ferramentas inversas, ok?
Então, vamos calcular isso aí:
Estamos integrando em , ou seja, tudo o que está mltiplicando o passa a ser uma constante e integramos apenas o próprio :
OBS: Essa constante é adicionada por se tratar de uma integral indefinida, ou seja, sem nenhum limite de integração.
Para encontrarmos o valor dessa constante , podemos usar o fato de que no tempo já conhecido o corpo se encontrava parado, ou seja:
Assim, temos que:
Então, a nossa expressão para vai ser isso tudo junto e misturado:
Tá vendo que aqueles termos em parêntesis que multiplicam os “t”s são iguais?
Então, podemos agrupar eles somando os “t”s:
Melhorando só mais um pouquinho, podemos colocar em evidência o e também já podemos escrevê-lo como vetor na direção horizontal positiva :
Mas como queremos esse vetor no instante , basta aplicar esse valor no lugar do :
Pronto, achamos a velocidade!
Agora só falta o vetor posição .

Vamooo, não desiste!
Passo 12
Como a velocidade é a variação da posição , ele é sua derivada:
Então, vamos usar a mesma estratégia de antes, mas vamos integrar a expressão antes de substituir a constante :
Lembrando, todos os termos que não são “” vão funcionar como constantes, então integramos apenas os “t”s, adicionando novamente uma outra constante no final:
Para achar essa constante , vamos usar novamente o fato de que o corpo estava parado no instante conhecido , ou seja sua posição ainda era zero:
Passo 13
Agora, vamos escrever colocando esse valor de :
Novamente, temos vários termos parecidos, vamos tentar juntar isso ai:
Substituindo , temos:
Agora, vamos simplificar isso.
Passo 14
Para não ficar mais imenso do que já está, vamos multiplicar apenas o termo de dentro dos colchetes pelo termo lá no final:
Agora, vamos juntar todos os termos com , vamos até colocar um no lugar dos outros termos para focarmos no que estamos mexendo por enquanto:
Lembrando de ajustar os sinais, pois estamos colocando todos os termos em evidência juntos:
Podemos tirar o MMC e colocar em evidência a constante :
Botando o sinal de menos em evidência, podemos colocar na forma de um produto notável:
Então, ficamos com:
Essa é aquela hora que a gente já começa a se perguntar:

Mas churumelo, estamos no último pequeno passo.
Vambora!
Passo 15
O que a gente fez foi achar o vetor posição (com muito sofrimento rs), para um instante qualquer .
Lembrando que esse cara é um vetor na direção horizontal, então ele tem a componente :
Então, agora basta substituir o qualquer pelo instante que queremos :
Colocando o dos termos , ficamos com:
Achamos a resposta!

Resposta
(a)
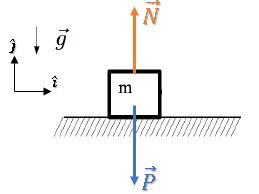
(b)
Entrar em movimento:
Perder contato com o solo:
(c)