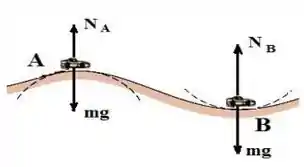
Parte II - Na figura abaixo um carro se desloca com velocidade de módulo constante ao longo de toda a trajetória sobre uma elevação circular de raio e em seguida em um vale circular com raio . Sabendo que na parte inferior do vale a força normal do assento sobre o motorista vale , determine a força normal experimentada pelo motorista ao passar pelo ponto mais alto da elevação. O peso do motorista é .
Passo 1
Parte II
- Calculando a força normal em A:
Em A, a força centrípeta é dada por:
Por que o peso aponta pra dentro da curva e a normal pra fora
Em B, a força centrípeta é dada por:
Agora a normal aponta pra dentro da curva e o peso para fora.
Substituindo (2) em (1):
Resposta
Parte II
Exercícios de Livros Relacionados
Calcule a aceleração inicial para cima de um foguete de massa 1,3×10 4k g se a força inicial para cima produzida pelos motores (empuxo) é 2,6×10 5N e o foguete parte do nível do mar. Não despreze a fo
Projeto pista de pouso. Um avião de carga decola de um campo plano rebocando dois planadores, um atrás do outro. A massa de cada planador é de 700k g , e a resistência total (arraste do ar mais atrito
Um foguete de teste de 2540k g é lançado verticalmente da plataforma de lançamento. Seu combustível (de massa desprezível) provê uma força propulsora tal que sua velocidade vertical em função do tempo
A Queda da Genesis. Em 08 de setembro de 2004 , a espaçonave Genesis caiu no deserto de Utah porque seu paraquedas não abriu. A cápsula de 210k g atingiu a Terra a 311k m / h e penetrou o solo a uma p
O motor de um foguete de 125 k g (incluindo toda a carga) produz uma força vertical constante (a propulsão) de 1720 N . No interior desse foguete, uma fonte de energia de 15,5 N está em repouso sobre