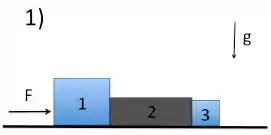
Sejam 3 blocos colocados em um plano horizontal sem atrito. Suas massas são , e . Um força é aplicada sobre o bloco , como na figura 1. Em todos os itens a seguir desconsidere todos os tipos de atrito. Considere .
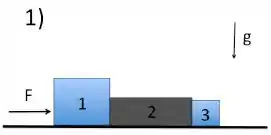
a) Faça o diagrama de forças para cada um dos blocos. Calcule a aceleração de cada bloco (figura 1).
b) Calcule as forças entre cada bloco (figura 1).
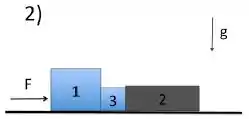
c) Alterne a ordem dos blocos e (figura 2) e calcule o valor de todas as forças entre os blocos na nova situação.
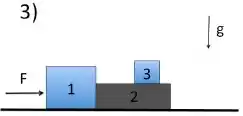
d) Na situação exata da figura 3, calcule as novas acelerações dos 3 blocos.
Passo 1
Na letra (a), queremos o diagrama de forças em cada um dos blocos (figura 1) e depois queremos suas acelerações.
Vamos começar com o diagrama de forças.
Para todos eles, teremos uma força peso apontando para baixo e uma força normal para cima.
Além disso, existirão forças de contato entre os blocos.
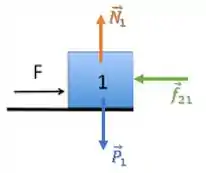
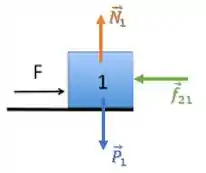
Bloco 1:
O bloco 1, devido à ação de , está empurrando o bloco 2.
Assim, o bloco 2 devido ao princípio da ação e reação, empurra de volta o bloco 1 com .
Então, as forças aplicadas sobre o bloco 1 são:
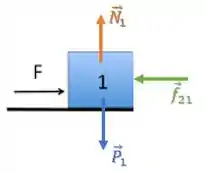
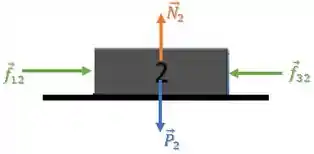
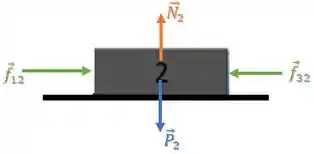
Bloco 2:
O bloco 2 está sendo empurrado pelo bloco 1 através da força .
Por sua vez, ele empurra o bloco 3, logo o bloco 3 empurra de volta o bloco 2 com uma força .
Então, as forças aplicadas sobre o bloco 2 são:
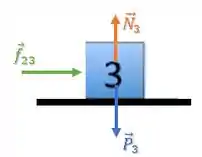
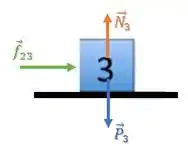
Bloco 3:
O bloco 3 está sendo empurrado pelo bloco 2, através da força .
Então, as forças aplicadas sobre o bloco 3 são:
Passo 2
Agora, vamos achar as acelerações.
Como um bloco está empurrando o outro, eles não perderão contato ao longo do movimento.
Assim, eles estarão andando juntinhos e por isso terão a mesma aceleração:
Além disso, vamos considerar como o nosso sistema os três blocos.
Assim, essas forças de contato entre os blocos serão forças internas onde uma anula a outra, já que sempre existe o par de ação e reação.
Então, a única força externa atuando sobre os bloquinhos na horizontal é .
Então, podemos aplicar a Segunda Lei de Newton, considerando esses três blocos como um blocão só de massa igual à soma das três massas:
Passo 3
Na letra (b), queremos as forças entre cada bloquinho.
Uma vez que já temos a aceleração de todos os blocos , fica mais fácil.
Basta agora considerarmos como nosso sistema cada bloco individualmente e aplicar a Segunda Lei de Newton.
Vamos utilizar també o fato de que um bloco aplica num segundo, apresenta o mesmo módulo da força que esse segundo aplica no primeiro.
Então, os pares de ação e reação são:
Força de contato entre o bloco e o bloco :
Para achar essa força, podemos analisar o bloco 1.
Aplicando a Segunda Lei de Newton, temos:
Substituindo os valores, temos:
Esse será o módulo da força entre eles, ou seja:
Força de contato entre o bloco e o bloco :
Para achar essa força, podemos analisar o bloco 3.
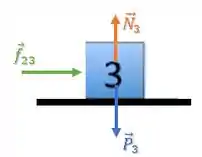
Aplicando a Segunda Lei de Newton, temos:
Ou seja:
Passo 4
Na letra (c), queremos achar as forças sobre entre os blocos para a nova situação da figura 2:
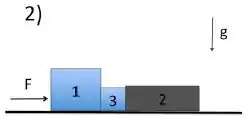
Para isso, vamos fazer o mesmo procedimento que fizemos na situação 1.
Primeiro, vamos achar a aceleração do conjunto, já que os blocos andam juntos:
Assim, podemos ver que a aceleração não se alterou apesar da mudança na ordem dos blocos:
Passo 5
Entretanto, vamos dar uma olhada nas forças entre os blocos.
O diagrama de corpo livre do primeiro bloco continuará o mesmo. A única mudança será o nome da força que agora está sendo exercida pelo bloco 3.
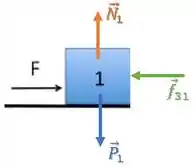
Aplicando a Segunda Lei de Newton para o primeiro bloco:
Achamos que a força de contato entre os blocos e é:
Para descobrir a força entre os blocos e , vamos fazer o novo diagrama de forças no bloco e aplicar a Segunda Lei de Newton.
Como ele está na ponta, a única força atuando sobre ele na horizontal será:
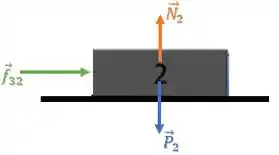
Então, a força de contato entre os blocos e é:
Passo 6
Na letra (d), queremos a aceleração de cada bloco na nova configuração da figura 3:
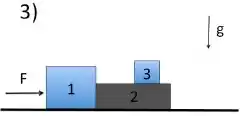
Agora, temos que tomar muito cuidado para não sair fazendo a mesma coisa que nos outros itens.
O que há de diferente?
Repare que vai existir uma força de contato entre os blocos e :
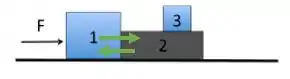
Entretando, não há nenhuma força horizontal atuando sobre o bloco .
Como não há nenhuma espécie de atrito entre as superfícies, o bloco vai delizar sobre o bloco , continuando em repouso, enquanto os blocos e vão se movimentar para a direita.
O diagrama do corpo ficará da mesma maneira:
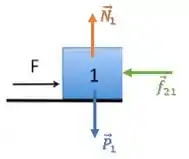
Já o diagrama do corpo terá mais uma força de contato na vertical:
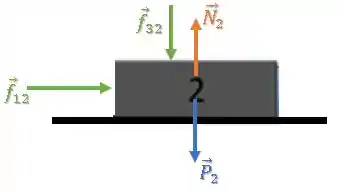
Ficamos com um sistema assim:
Já vimos que as forças entre os blocos e são iguais em módulo:
Então, vamos subtituir o valor de da segunda equação na primeira:
Assim, chegamos na mesma expressão que teríamos se considerássemos os blocos e como um corpo só de massa e aplicássemos a Segunda Lei.
Colocando os valores numéricos:
Como os blocos e andam juntos:
Já o bloco 3 permanece em repouso:
Resposta
(a)
(b)
(c)
(d)