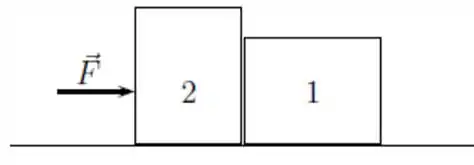
A figura mostra dois blocos, 1 e 2, de massas e , respectivamente, em contato sobre uma mesa horizontal sem atrito. O movimento é unidimensional. Se é a força com que o bloco de massa é empurrado, é a força com que o bloco 2 empurra o bloco 1, a razão entre os módulos é
(a)
(b)
(c)
(d)
(e)
Passo 1
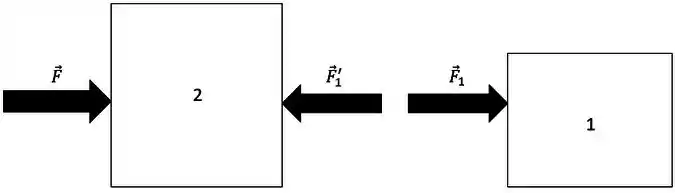
Vamos fazer o diagrama de corpo livre dos blocos pra ver as forças que estão atuando neles.
Mas como ele disse que o movimento é unidimensional, vamos ignorar as forças agindo na vertical (peso e normal), ok?
Então tem a força , que age no bloco 2 e a força , que o bloco 2 faz no bloco 1. E pela 3ª lei de Newton, também tem a força de reação , de mesmo módulo que , que o bloco 1 faz no 2.
Passo 2
Então o diagrama de corpo livre dos blocos é:
Passo 3
Vamos começar focando no bloco 2. Nele agem as forças e , então a força resultante agindo nele é:
E como o bloco está indo pra direita, em módulo isso fica:
E pela 2ª lei de Newton,
sendo o módulo da aceleração do bloco 2.
Logo,
Passo 4
Vamos fazer a mesma coisa com o bloco 1! A única força atuando nele é :
E aplicando de novo a 2ª lei de Newton:
sendo a aceleração do bloco 1.
Então
Passo 5
Beleza, obtivemos duas equações:
Mas espera, os blocos estão andando juntos, então eles têm a mesma aceleração!
Então o nosso sistema ficou mais simples:
Passo 6
Substituindo a 2ª equação na 1ª :
Então agora já dá pra gente calcular a razão entre e :
Resposta
Alternativa (e)