P1 de Cálculo 1 da USP - 2018

b) Calcule, caso existam, os seguintes limites:

a) Calcule, caso existam, os seguintes limites:

Dada a seguinte função

Então:

1. é contínua em e derivável em
2. é contínua em e não derivável em
3. não é contínua em e não derivável em
4. não é contínua em e é derivável em

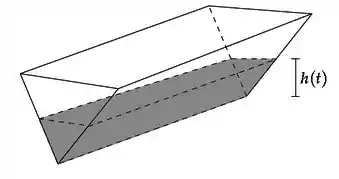
Uma mangueira está enchendo um tanque com água. O tanque tem o formato de um prisma de comprimento cuja base é um triângulo equilátero (ver figura abaixo). Sabendo que a vazão é constante e igual a , determine a taxa de variação da altura da água, no instante em que ela é .

Seja uma função derivável num intervalo aberto que contém e tal que

Para todo . A equação da reta tangente ao gráfico de no ponto é:

c) Calcule, caso existam, os seguintes limites:

Considere a seguinte função dada por:

Os valores reais de e que tornam contínua são:

1. e
2. e
3. e
4. e
5. e

Sejam tais que então:

1. Teremos sempre que
2. Teremos sempre que
3. Podemos ter
4. Teremos sempre que
5. Podemos ter

Seja satisfazendo a seguinte propriedade

Então podemos afirmar que:

1. Existe tal que, para todo , temos
2. está definida para todo
4. Existe tal que, para todo , vale
5. Existe tal que, para todo , vale