c) Calcule, caso existam, os seguintes limites:

A primeira coisa que a gente tem que notar nesse limite maluco é que temos um polinômio no interior do seno! Ok mas e dai? Veja bem, se tivermos algo do tipo:

Podemos fazer a substituição:

E esse limite seria reescrito para o famoso e querido limite fundamental trigonométrico:

Então vamos tentar reescrever o limite pra deixar um pendurado. Multiplicando em cima e em baixo por , temos:

Usando as propriedades dos limites, temos que:

Como um desses limites é o limite fundamental trigonométrico, a gente resume o limite do enunciado para:

Nesse passo vamos calcular o limite sem o seno e depois partir pro abraço, beleza? Infelizmente ainda não dá pra calcular direto porque:

Vamos manipular os polinômios então. Começando pelo numerador, que nada mais é do que uma diferença de quadrados! Usando o produto notável:

Reescrevemos o limite para:

Beleza, agora o denominador. Infelizmente esse vai ser um pouco mais complicado porque não tem produto notável que resolva. Mas como sabemos que é uma raiz, podemos fazer Briot-Ruffini, não é mesmo? Então vamos lá. Seguindo os passos: colocamos a raíz na casa mais a esquerda e escrevemos os coeficientes de cada potência de em ordem decrescente de potência. Ficamos com:

2

1

-5

8

-4

Descemos o primeiro termo pra casa de baixo, multiplicamos pela raiz e somamos ao coeficiente seguinte, colocando o resultado na casa do lado. Vamos ficar com:

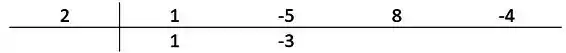
Repetindo o procedimento com o , vamos multiplicar pela raiz e somar ao , colocando o resultado logo abaixo do . Vamos ter:

E fazendo a mesma ideia de novo, completamos a última casa com:

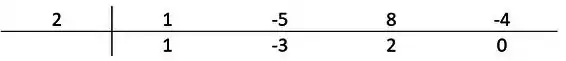
Opa, resto zero, quer dizer que realmente não vamos ter números pendurados e, sendo os números encontrados os coeficientes do polinômio de grau 1 unidade inferior (no caso, 2), podemos reescrever o polinômio de terceiro grau como:

Ok, mas ainda não acabou, porque o limite vai ficar reescrito para:

O que continua dando indeterminação. Puts, mais contas então! Nesse caso, vamos ter que pegar esse polinômio de segundo grau e simplificar ele ainda mais. Como é de segundo grau, podemos usar Bháskara! As raízes de:

Vão ser então:

Opa, maravilha, poderemos reescrever então o polinômio como:

E o limite vai ser reescrito pela última vez para:

E agora fechamos a questão! Quer ver? Dá uma olhada:

Como:

E estamos tendendo por valores menores que , vai valer o segundo caso. Ficamos com:

E prontinho! Indeterminação foi-se embora! Calculamos direto o limte para:

Ufa, cabamos! O limite finalmente foi encontrado e será: