Seja satisfazendo a seguinte propriedade
Então podemos afirmar que:
- Existe tal que, para todo , temos
- está definida para todo
- Existe tal que, para todo , vale
- Existe tal que, para todo , vale
Passo 1
(a) Existe tal que, para todo , temos
Vamos analisar bem essa letra: Ela diz que o módulo da função é sempre menor que um valor qualquer positivo. Mais na prática, o que isso quer dizer? Vamos lembrar direitinho o que é um módulo. Saca só:
Se aplicarmos isso à inequação, vamos ter:
Ou seja, se , então:
Uma função que satisfaz isso é e ainda satisfaz as condição do enunciado, dá uma olhada:
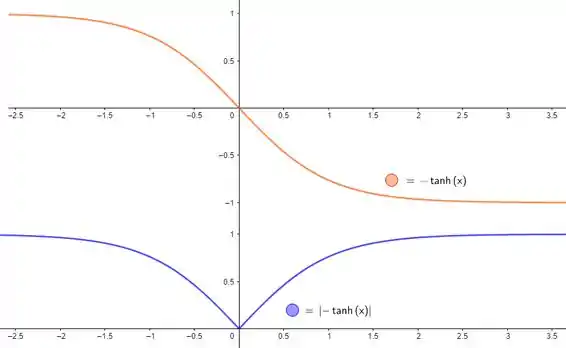
No entanto, é possível uma função ter o limite do enunciado e não necessariamente estar confinada entre e . Quer ver? Dá uma olhada nesse exemplo da função :
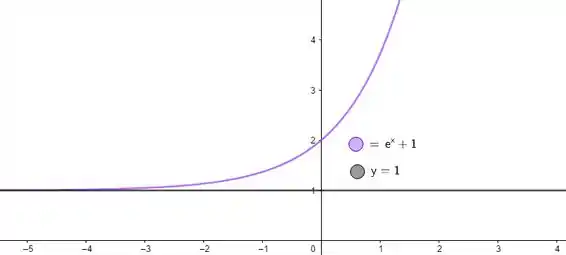
E olha só! O módulo dessa função é inclusive ela mesma, já que a função é sempre positiva! Essa função de fato satisfaz o limite imposto pelo enunciado e desmente a letra que, vimos então, ser falsa.
Passo 2
(b) está definida para todo
Vamos lá, próxima letra. Primeiro, vamos lembrar que significa a inversa de . Vamos estudar a primeiro então, com base no enunciado. Se o limite do enunciado é uma verdade:
Então está definido para todo . Agora falando sobre funções inversas: elas possuem como contradomínio o domínio da função que a deu origem. Dá uma olhada nesse exemplo:
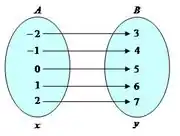
Onde é o domínio de e é o contradomínio. Agora, pra sua inversa , temos:
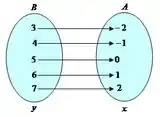
Onde é o domínio de e é o contradomínio de . Show, em outras palavras então, pra ter domínio incluindo valores negativos, o contradomínio de tem que conter valores negativos também!
Buscamos então uma função que tenha o limite do enunciado e que assuma valores de . Um exemplo é a função , que tem inversa :
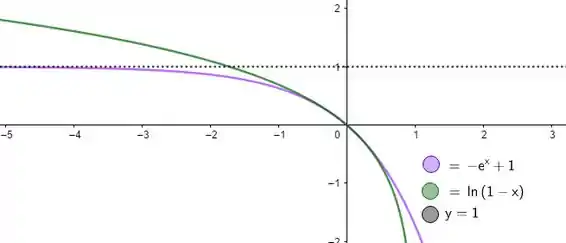
Mas saca só: o mesmo contraexemplo da letra prova que a também está errada! Veja, a função satisfaz o limite do enunciado, mas por não existir nenhum valor de que faça nesse caso, então a inversa não vai estar definida pra ! Sendo a inversão dessa vez , temos:
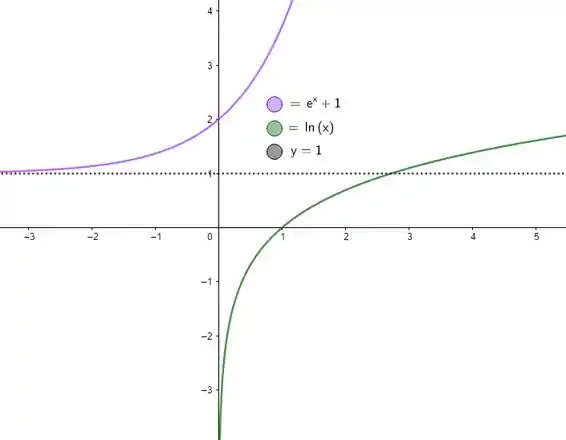
Passo 3
(c)
Aqui de novo a gente pode usar o exemplo da função . Não é porque uma função tem uma assíntota pra que necessariamente ela vai ter assíntota pra ou que, se tiver, vai ter o mesmo valor. Como mostrado na letra , tanto quanto são exemplos de funções que satisfazem o enunciado:
Mas a primeira não tem assíntota horizontal pra e a segunda função tem, mas é uma assíntota diferente de
Passo 4
(d) Existe tal que, para todo , vale
Agora o caso é o seguinte: queremos um negativo qualquer em que a função seja positiva e que continue assim pra qualquer número menor que esse negativo. Veja bem, se o limite do enunciado:
É positivo para , então quer dizer que é de fato maior que quando é negativo! Mas isso talvez não valha para pra qualquer , saca só esse exemplo:
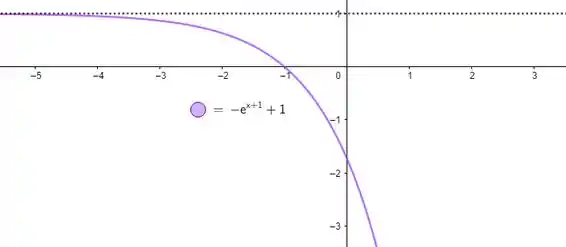
Nesse exemplo, temos que . Mas mesmo que a função não corte o eixo , não torna o enunciado inválido! Quer ver? Vamos pegar o mesmo exemplo que usamos várias vezes:
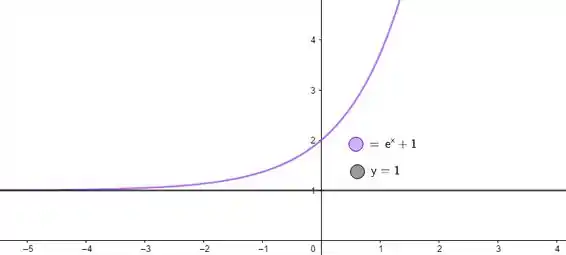
Se eu escolher qualquer que eu quiser, o enunciado continua verdade. Exemplos
E por aí vai. Então achamos nossa letra correta!
Passo 5
(e) Existe tal que, para todo , vale
Letra semelhante a anterior. Essa questão vai ser falsa porque ela implica que toda função que satisfaz o limite do enunciado:
Necessariamente tende à de baixo pra cima, como é o caso do exemplo . Maaas, como existe exemplos de que tendem à de cima pra baixo, como o caso do tão repetido exemplo , essa letra vai ser então falsa!