Uma mangueira está enchendo um tanque com água. O tanque tem o formato de um prisma de comprimento cuja base é um triângulo equilátero (ver figura abaixo). Sabendo que a vazão é constante e igual a , determine a taxa de variação da altura da água, no instante em que ela é .
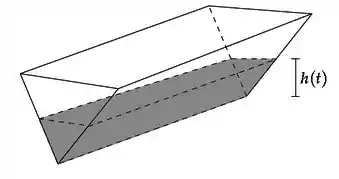
Passo 1
Essa questão parece complicada mas relaxa que a gente tira de letra. Vamos rever as informações que nós temos:
- Vazão
- Comprimento do tanque
- Instante da altura
Vamos olhar pra primeira informação. Se as unidades de vazão são , e é unidade de volume, temos então que:
Esse volume vai ser volume de líquido. E veja bem, independente da taxa de aumento do volume, o formato da água vai ser sempre o mesmo: um prisma de base triangular! E o volume de um prisma deitado desse tipo vai ser dado por:
Onde é a área lateral, ou seja, a área do triângulo equilátero e é o comprimento. Como o comprimento é dado e vai ser fixo enquanto a água aumenta, vamos ter que:
E derivando em relação ao tempo:
E olha só! , que é a vazão, é dado do problema também! Sendo assim, substituímos e temos:
Descobrimos como a área lateral do prisma de água varia com o tempo, mas não é bem isso que queremos né? Vamos tentar relacionar então com
Passo 2
Olhando pra base do prisma de água, vemos que ele é um triângulo equilátero.
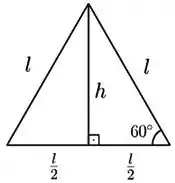
Como qualquer triângulo, a área desse triângulo vai ser:
Como essa área é a área lateral do prisma de água, que é uma função do tempo, e representando o triângulo da forma que a figura do enunciado nos dá, temos então que:
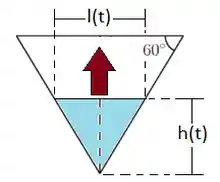
Onde a seta vinho indica o sentido da variação do nível de água.
Beleeeza, mas temos um problema: não sabemos e nem queremos saber nada sobre . O jeito então vai ser relacionar com que é o protagonista dessa nossa questão. Uma forma é a gente pensar em trigonometria! Como o triângulo é equilátero, todos os ângulos são de ! Sendo assim:
A área lateral em função do tempo vai ser então:
Passo 3
Agora que sabemos a cara de , vamos precisar derivar beleza? Afinal, sabemos ! Derivando, vamos ter:
Juntando com o valor de encontrado no passo , temos:
Não acabou ainda. O enunciado quer a taxa de variação da altura do nível de água, mas não é a taxa de variação em qualquer instante não em! Ela quer em un determinado instante em que . Sendo assim, vamos ter:
Fechouuu! A taxa de variação da altura do nível de água vai ser então: