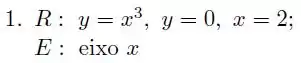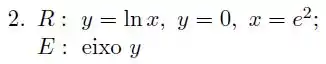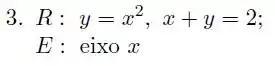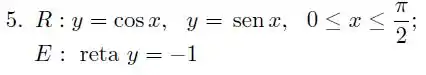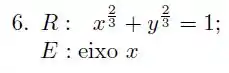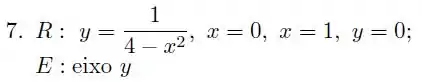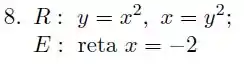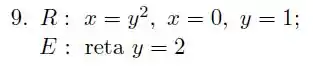Listas GMA de Cálculo IIA da UFF - Lista 6
Cálculo IIA - UFF
Considere a região limitada pelas curvas de equações dadas. Aplicando o método dos discos circulares, calcule o volume do sólido obtido pela rotação da região em torno do eixo dado:
Ver solução completaEm cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Aplicando o método das cascas cilíndricas, calcule o volume do sólido obtido pela rotação da região em torno do eixo dado.
Ver solução completa
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Calcule, por dois métodos distintos, o volume do sólido obtido pela rotação da em torno do eixo dado.
Ver solução completa
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Calcule, por dois métodos distintos, o volume do sólido obtido pela rotação da em torno do eixo dado.
Ver solução completa
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Calcule, por dois métodos distintos, o volume do sólido obtido pela rotação da em torno do eixo dado.
Ver solução completa
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Calcule, por dois métodos distintos, o volume do sólido obtido pela rotação da em torno do eixo dado.
Ver solução completa
Calcule o volume do sólido obtido pela rotação da região em torno do eixo , pelo método que achar mais conveniente.
Ver solução completaQuando giramos o gráfico de uma função de classe , , , em torno do eixo , obtemos uma superfície de revolução, cuja área é definida pela integral
(para maiores detalhes, veja o livro do Stewart vol. , seção )
Calcule a área da superfície de revolução obtida pela rotação em torno do gráfico de cada função indicada. Faça um esboço da superfície.
Ver solução completa
Quando giramos o gráfico de uma função de classe , , , em torno do eixo , obtemos uma superfície de revolução, cuja área é definida pela integral
(para maiores detalhes, veja o livro do Stewart vol. , seção )
Calcule a área da superfície de revolução obtida pela rotação em torno do gráfico de cada função indicada. Faça um esboço da superfície.
Ver solução completa